Embryology Biology 441 Spring 2013 Albert Harris
How mechanical forces cause geometrical shapes
Genes -----> Forces -----> Anatomy
Fluid interiors pushing out, inflating flexible surfaces.
Here are sixteen examples. Please try to think of more. Let's try for 20.
#1) Hollow blastulas (sea urchins) and blastocysts (mammals) are examples.
#2) The brain, and the rest of the central nervous system, are a hollow, fluid filled tube.
The pressure of this cerebro-spinal fluid inflates the brain more than the spinal cord.
Lobes of the brain are created by more inflation at certain places than elsewhere.
A simple experiment is to poke a small hole in any part of the neural tube, and reduce the pressure to near zero. Insertion of a hollow glass tube will prevent the hole from closing. This results in the brain lobes not inflating.
#3) The eyeball is inflated with a weak gel, which acts like a liquid. Inserting a hollow glass tube through the eyeball will prevent its inflation. (Dr. Coulumbre proved this, at the NIH)
#4) Teleost oocytes form their upward-bulging blastodisk by cytoplasmic pressure pushing against a circle where the contractility of the cell cortex is weaker than elsewhere.
#5) Cleavage (cytokinesis) of all animal cells is caused by strengthening of cytoplasmic acto-myosin in the circumferential direction in a belt-like contractile ring that pinches the cell in two after mitosis (And separate from the mechanism of chromosome movement in mitosis).
#6) Polar body formation is a special unequal form of cytokinesis, that follows each meiotic division of oocytes.
#7) Cartilages expand by electro-osmotic pressure pushing outward against resistance of collagen and elastin fibers. These fibers wrap around the outside of each cartilage, and also run through the interior of the cartilage. Visualize water balloons with very gooey water inside, and with nylon threads and rubber bands wrapped around the outside, and also running through the interior.
The shapes of the bones that will later replace cartilages are created by directional differences in cartilage swelling. "Long bones" get their shapes from resistance to swelling being stronger in the circumferential direction, and weaker in the direction of greatest elongation.
NOTE: To the extent that the outward swelling pressure is osmotic, this pressure is not capable of being stronger in one direction than in any other direction.
(Ask yourself: can a concentration of ions be stronger in one direction than another? Hint: No)
Chemical concentrations can easily be larger in some places than others, but can't be larger in any direction than another.
Be careful not to confuse this with chemical gradients, in which concentrations change from place to place.
Gradients DO have directions; (they are vector quantities)
Concentrations CAN'T have directions. (they are scalar quantities)
More later about directionality of quantities.
#8) Notochords are tightly packed with weak, vacuolated, jelly-like, cells; and are tightly wrapped with sheets of collagen fibers, running in spirals.
#9) Blood vessels (arteries, veins, capillaries) are lined with a special kind of thin epithelial cells named "endothelial cells", which are wrapped by collagen fibers, smooth muscle cells, and fibroblasts. It's an unasked mystery what mechanism wraps them with collagen. Another is why smooth muscle cells orient circumferentially; perpendicular to what contact guidance usually produces!
#10) The chambers of the heart;
#11) kidney ducts and glomeruli;
#12) salivary glands;
#13) pancreatic acini & ducts;
#14) alveoli and bronchi of the lungs;
#15) tentacles and buds of hydra;
#16) excurrent canals of sponges;
I hope you now agree that embryology needs whatever mathematical concepts, tools, vocabulary or methods help us think cumulatively & make sense of counter-balances between fluid pressures and stretched surfaces. I promise these first steps won't be difficult or require equations.
HERE WE GO...
Tensions are not scalars, and they are not vectors either.
They belong to another category of variable, which differs from a vector as much as a vector is different from a scalar.
Many important variables belong to this new category:
(which is to a vector as a vector is to a scalar).
The curvature of surfaces belongs to this other category of variable.
The distortion of a compressed, twisted or stretched material belongs to this category.
The elastic resistance of pieces of materials also belongs to this other category.
Many other physical variables belong to this other category. Not vectors; not scalars!
Try to imagine a gradient of a vector! Would it be another vector? Or what?
Scalar variables have an amount at each location in space.
Vector variables have an amount and a direction at each location.
The new kind of variable has an amount in each direction at each location.
The first such variable that mathematicians analyzed was tension (and compression, which equals negative tension)
So they named the whole category of variables "tensors"
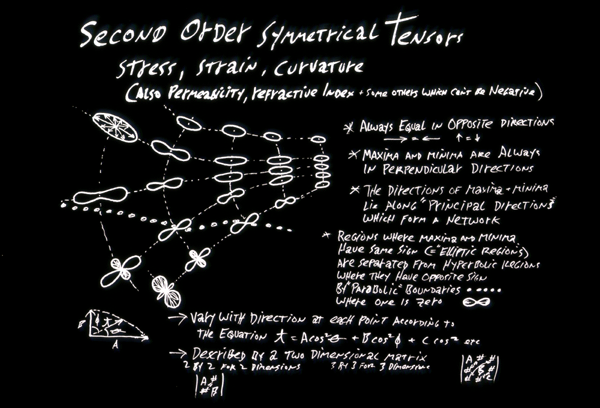
Tension (equals "stress") is a tensor. (a symmetric tensor of the second order)
Strain (distortion) is a tensor. (a symmetric tensor of the second order)
Elastic resistance is a tensor. (a symmetric tensor of the fourth order)
Notice that they didn't invent new words for third, fourth, fifth order tensors!
In fact, vectors are classified as first order tensors & scalars as zeroeth order tensors!
A ratio of a second order tensor to a third order tensor would be a fifth order tensor. (You add the numbers of the orders)
Elastic resistance is the ratio of stress to strain. 4 = 2 + 2
Don't worry too much about the following small fact, which I hope may give you some sense of direction: Tensor variables differ as functions of direction according to certain equations (which I won't even tell you, lest you memorize them), which contain either the cosine of the directional angle, or the cosine squared of that angle, or the cosine cubed, or the cosine to the fourth power, etc. Fourth order tensors vary as the fourth power of the cosine of the directional angle; Second order tensors vary as the cosine squared, etc. An interesting consequence is that except where curvatures and tensions happen to be the same in all directions (spheres, planes, etc.) then for any second order tensor their maximum directions are always exactly perpendicular to their minimum directions. However much it seems as if surely you could carve a block of soap, or twist a block of rubber, such that curvatures and stresses wouldn't have maxima perpendicular to minima, it's logically impossible.
Just because a tensor variable can in principle vary with direction, it doesn't have to.
That is NOT logically impossible. A sheet of elastic material can easily have the same amount of tension everywhere, and also the same in every direction.
Soap bubbles are a good example. Another is the surface tension of droplets of liquid.
Tensions at their surfaces are caused (and resisted) by tendencies of liquids to leave the surface and move into the liquid.
When a liquid molecule leaves a surface, it goes inward, not sideways.
Therefore, equal tension is created in all directions. It can't produce more tension in one direction than another. For soap films, that's another logical impossibility.
Notice that balloons are different. The tensions at their surfaces are caused by stretching rubber. These tensions can be different in one direction from another, and also different from one place to another. But maxima and minima still can't help being perpendicular.
Living cells, with actively contractile cortical layers of "cytoplasmic actin and myosin" are capable of even more variation than soap bubbles. The same is true of sheets of living cells. This free ability to vary includes the ability to contract with equal strengths in all directions and at all locations. That will cause cells and groups of cells to behave as if they had a "surface tension". Many scientists have mistakenly concluded that isotropic contraction must be caused (literally) by surface tension.
"How do you KNOW she is a witch?"
'She is made out of soap!'
D'Arcy Thompson mistakenly persuaded himself and his readers that self-building shapes can only result from tensions that don't vary with direction; others believe that convergence to any consistent geometry, via two or more alternative sequences of intermediate geometries, can only be caused by forces that are reversible, conservative and minimize free energy. Mathematicians tend to think that they somehow "own" the concept of tensors, think of them more in the sense of "transformation of number matrices", not as physical variables, and prefer biologists not to use them. Better they should be helping us understand extracellular matrices.
Incidentally, tensors played a major role in the escape of physics from the "ether" concept, which was analogous to "positional information" in today's embryology.
Some engineering and mathematical concepts embryologists need. (& 99% of biologists never learn about)

Stress = mechanical force per cross-sectional area: Either tensile stress or compressive stress
It has units of force per unit area .
Strain = proportional stretching or compression (produced by stresses)
What % has a material lengthened or shortened. (or sheared)
If all stresses were relieved, then how much would dimensions change
Young's modulus = the slope of the curve of stress per strain
Rubber has a small Young's modulus; Steel has a large one
Hooke's law = linear proportionality of stress to strain
If Young's modulus is constant, then a material is "Hookean"
But real materials are never Hookean beyond 1 or 2% strain.
Please understand that Hooke's law is NOT a law of nature.
It is a rule of thumb that is sometimes true.
At small strains (<1 or 2 %) it is true of many materials.
At large strains (>10% it is always more and more untrue)
Also, when Hooke's Law is not obeyed, then
Young's modulus is not constant, & so doesn't really exist.
It's a proportionality constant for a ratio that isn't constant;
or the slope of a curved line (sometimes one with hysteresis!)
(hysteresis in the sense that the pull is stronger for a given % strain when you are applying force, but weaker as you release this stress)
SOME EQUATIONS WE WILL TALK ABOUT TODAY ARE EXACTLY TRUE.
Others are approximations. Hooke's Law is a useful approximation, but if the walls of your arteries obeyed this law (exactly) you would die of aneurisms!
The curvature of surfaces and layers may be the single most important variable for us to understand, in relation to shape.
Curvature = angular change of the tangent line per distance
(angular change per distance along a curve)
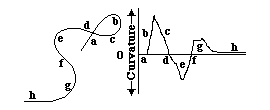


The Radius of Curvature = 1 / divided by curvature
(and has units of distance per radian of angular change)
(also, it is the radius of the circle that would most closely approximate a given section of a curve)
A straight line has zero curvature.
(and its radius of curvature is infinite, please notice)
A circle has constant curvature.
Curvature of small circles is larger than curvature of big circles.
A sphere has constant curvature in all directions .
A plane has zero curvature in all directions.
What is the curvature of the surface of a cylinder?
...of the surface of a cone?
...of the surface of a lemon?
...of the surface of an eyeball?, or a lens?
A cylinder has zero curvature in the lengthwise direction;
and has constant curvature in the circumferential direction.
Curvature of surfaces varies with direction,
for all shapes except for spheres or planes
(on which curvature is the same in all directions)
It turns out that stress and strain also can vary with direction.
And elastic moduli vary even more with direction.
(even if they happen to be constant in a given direction)
Differential Geometry is a division of higher mathematics in which shapes are defined in terms of curvatures, instead of the x, y, z coordinates that we learn about in elementary mathematics.


Stress, strain and curvature (of surfaces)
All 3 happen to be Tensor variables of the second order.
You know something about vectors, right?
You know vector variables have a direction as well as an amount;
in contrast to scalar variables, which have an amount at each place.
Examples of scalar variables: temperature, chemical concentrations
(also osmotic pressure, & water and gas pressures)
[assuming we can ignore wind or currents]
Examples of vector variables: wind speed, magnetic force
(Also gradients of scalar variables are vectors)
Vectors can (correctly!) be regarded as tensors of the first order.
Scalar variables are regarded as tensors of zero order.
Stress, strain and curvature are tensors of the second order.
Elastic moduli are tensors of the fourth order.
(I think maybe birefringence is a tensor of the third order)
(and there are properties that are 5th, 6th etc. order tensors)

Do not be frightened by tensors. They are your friends.
A little knowledge of tensors is useful for intellectual self-defense.
A stretched string can exert sideways pressure
Tension * Curvature = sideways force P=T*C
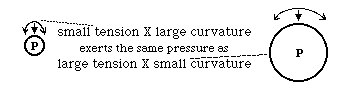
"Tension" means the same thing as tensile stress.
Pressure across a flexible sheet of material obeys this equation:
Pressure = T * C + t * c
Because tension and curvature can vary with direction,
T & C the values in one direction,
t & c in the perpendicular direction
Really, it could be more accurate to take some kind of integral.
(there are better things to worry about than that, however)

For a soap film, the mechanism that generates the tension has the same strength in all directions: therefore: P = T * (C + c)
If we stretch a soap film across a curved ring, then P = 0
so C = -c Which is another way of saying that, at each location on the film, curvatures in perpendicular directions are exactly equal & opposite
The pressure inside a big bubble
is smaller than the pressure in a little bubble!!!
Inside any given bubble, Pressure is a constant at each part of the surface. Although stretching a bubble may cause this interior pressure to change, nevertheless P = T * (C + c)
so at each location, perpendicular curvatures vary inversely.
C + c = some constant
In a complex froth of bubbles, there will be different pressures in different bubbles, and curvatures will vary widely, but they will always obey these equations [EXACTLY]
The surface tension of bubble surfaces (and liquid interfaces) does not vary as a function of direction.
That is NOT true of a rubber sheet, or a balloon, or an eyeball, etc. much less of the surfaces of cells, or of epithelial sheets!
(Liquid and bubble interfaces are special cases, not a law of nature)
When tension can vary with direction, then P = T*C + t*c
and so C and c don't vary inversely by such simple rules,
but the rules are still simple enough to be very useful.
This equation controls the shape of the eyeball:
P = constant (because it's a fluid gel inside)
T has a lower (weaker) amount in the cornea than elsewhere.
therefore curvature is larger in the cornea (i.e. it bulges out)
If T in the cornea is made 1/3 as strong as in the sclera, then the curvature of the cornea will be 3 times larger than the sclera.
You let me control the Ts and Ps: I can make the Cs do what I want!
Even just controlling Ts, and letting P be some constant pressure, then the curvatures are almost completely at the mercy of the Ts.
Developmental biology is about how genes create & control anatomy.
Much is about how curvatures are created by tensions (acto-myosin)
The equations above cause the shape of the brain, the shape of cartilages (and thereby, the whole skeleton), the shape of limb buds, the diameters and branching patterns of blood vessels, etc. etc. etc.
This is very important for plastic surgery, & many other specialties.
To understand these issues (even a little) puts you way ahead of other future MDs.
Unfortunately, it is difficult to measure or map forces inside developing embryos, or to cause experimental changes in forces, or to predict exactly what differences are predicted by theories.
Much published research in this area has been based on fundamental mistakes, misunderstandings, and over-simplifications.
For example, the directional elongation of cartilage is claimed to be caused by directional secretion of matrix and growth of cells. Can you see why this is impossible and can't be the true explanation?
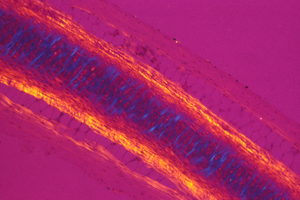
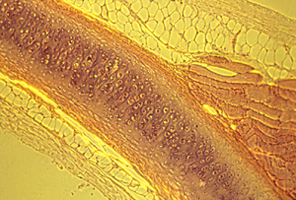
But the electro-osmotic pressure of cartilage is a scalar, which means it cannot possibly vary with direction. Pressure can vary from one location to another; and that can contribute to shape; but directional expansion has to be mostly caused by weakening of tension in one axis relative to tensions in the perpendicular axes.
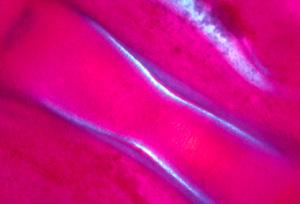

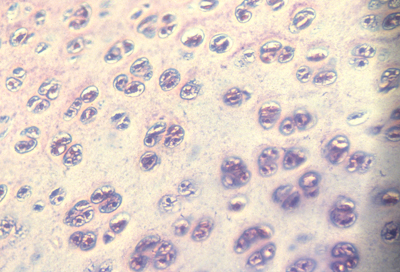



Reducing tensions inside embryos causes spatial irregularities and major birth defects, as extreme as doubling of organs.
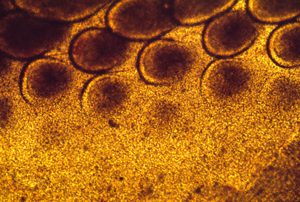
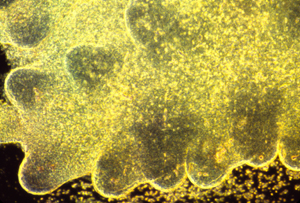
These photographs show the development of the embryonic rudiments of feathers in pieces of bird skin. When the skin develops normally, on the embryo's surface (or if it is kept under mechanical tension) then the feather rudiments form with highly-regular spatial periodicity. But when skin is cultured without the normal amount of mechanical tension, then the feather rudiments form at irregular positions.
On the surface of a soap film, or a balloon, in which the internal pressure is the same at all points on the surface, then pressure is equal to stress multiplied by curvature.
In other words, the local amounts of stress automatically adjust according to the local amounts of curvature , so that one multiplied times the other is a constant everywhere. To the extent that the material is flexible, & pressure is constant. If tension (= stress) becomes larger, then curvature becomes smaller.
Curves can be defined by the amount of curvature at each point. (Negative curvature means the line has curved back on itself.)
Polarized light is one of the only methods by which one can "see" the complicated geometric patterns of mechanical stresses inside developing embryos.

Although the following is beyond the scope of this course, you may be interested in knowing that one of the advantages of using mechanical forces for the direct control of anatomical patterns is that such mechanisms can directly optimize the geometrical arrangements of organs, for example in the branching patterns of blood vessels.

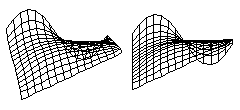
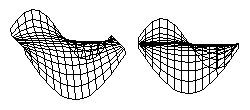
There is a classic problem in higher Mathematics called "Plateau's Problem" which is to calculate equations for the surface that has the minimum total area for a given perimeter. These diagrams show computer solutions for Plateau's Problem for an arbitrarily shaped edge. A soap film stretched across a wire will automatically "find" the shape that has the minimum total area. Any sheet of material that contracts with the same amount of tension in all directions will also "find" the shape with the minimum total area.
But if a sheet of material contracts with a stronger force in some directions than in other directions, then the shapes that it will form will be different than those formed by soap films. The shapes that are formed do not depend on whether the contracting layer is made out of soap, or rubber, or living cells. What matters is whether the tension varies with direction, or varies from place to place. If a layer of cells happens to contract with the same strength at each place, and in all directions, then the shapes it will form will be the same as would be formed by a soap film.
Unfortunately, when cell contraction happens to obey such simple rules, then many people say the force must be "surface tension". Textbooks often say this. But active contraction by actin and myosin can obey simple rules, or it can obey more complicated rules, in the sense of exerting stronger stress at some locations than others, or stronger stress in some directions than others. Such increased asymmetry of the forces exerted is a very effective way to create anatomical shapes. Most biologists have never learned the simplest concepts of tensor properties, or different kinds of symmetry. So when a contractile layer begins to contract more in one place that another, or more strongly in one direction than another, 99% of embryologists don't know how to think about what is happening.
The subfield of mathematics that finds shapes and equations that minimize or maximize some property is known as "The Calculus of Variations." So, Plateau's Problem is one of many problems that belongs to the calculus of variations.
The category of computer simulations that predicts (simulates) shapes and tension patterns that will be produced by materials as a result of obeying a given set of rules are called "Finite Element Methods." Although the actual materials you are interested in consist of infinite numbers of points, the computer simulation is based on a deliberately simplified, and finite, set of points with forces acting between them.
Millions of dollars are spent on finite element simulations of anatomical organs, and more research of this kind is needed. For example, some finite element simulations of sea urchin gastrulation and of neurulation in birds and amphibians have been published in embryological journals. (Google "George Oster").

Much further research is needed on this general topic. This research is being held back by mistaken theories that genes can only work by controlling the x, y, z coordinates where cells will differentiate. Sometimes, that's actually what happens (probably). But it's wrong to think chemical patterns always have to come first, and control mechanical and geometric patterns. But people who have never heard of differential geometry or tensors, but only studied about x, y, z coordinates, tend to assume that coordinates are the only possible way genes could create geometrical patterns.
Three-dimensional shapes of cells, whole organisms and of tissues and organs are created, controlled, changed, and healed in large part by means of adjusting contractile forces at cell surfaces (surfaces, layers of cytoplasmic actin and myosin just inside membranes), organ surfaces, and interfaces between cells and tissues.
A few examples,
-
1) the eyeball and cornea
2) lobes of the developing brain
3) chambers of the heart
4) cytokinesis (cleavage) of cells
5) osmotic swelling of cartilage and shaping of bone
6) inter-vertebral discs (and their herniations "slipping")
7) aneurisms of arteries
8) varicose veins
9) alveoli of lungs, branching of bronchi
10) branching angles of arteries
11) blastula formation, and many more examples.
For example by localized contraction of cytoplasmic actin cortexes adjacent to concave surfaces of invaginating cell sheets.
If you had a magic wand that could control surface curvatures, then you could change and create the shapes of everything.
More often, curvatures are indirectly controlled by adjusting stresses (tensions) and pressures
P = C*T + c*t
If you let me control the amounts of T and t, then can I control C and c?

Do I also need to control P?
There has been lots of unnecessary confusion on these issues.
One fact to get used to is that curvature can also be measured as "radius of curvature".
C = 1/R If you measure angles in radians, rather than degrees (a 180 degree angle is Pi radians)
A circle whose tangents change by 1 radian per centimeter has a radius of 1 centimeter.
I would have spared you this, except that biologists have mostly expressed surface curvatures in terms of radius of curvature; so you see equations like this
P = T/R +t/r or worse than that!: P = T (1/R + 1/r)
Do you see what's being slipped past us by this second equation above?
Tension is being treated as if it were a scalar variable, or a scalar CONSTANT!
For some special cases, like soap bubbles, T cannot vary with direction or location. (It is isotropic and homogeneous).
That also makes the math easier, but many people (including D'Arcy Thompson) mistook this special case for a general rule. (He didn't understand physics well enough to realize what he was assuming.)
Thompson could only explain a few special biological shapes. But he left almost everybody with the impression that he had exhaustively explored all the possibilities for creating biological shapes be means of surface tensions.
(It's as if Columbus had expected to discover new continents, but come back after finding Bermuda, & said that was all there was.
Consider specific questions:
Two soap bubbles, sharing a side; one bubble bigger than the other.
-
1) Is the side between them flat?
2) Or does the big bubble bulge into the smaller bubble?
3) Or does the smaller bubble bulge into the big one?
4) Does the answer differ from one try to another?
5) Would the answer be the same if two balloons shared a side?
-
5A) Flat side between them
5B) Big bulges into little
5C) Little bulges into big
5D) Result varies; depends on other factors? Is random? Unknowable?

What if two living cells, one bigger & the other smaller adhered along one side?
What if two blastulas shared a side; one bigger & the other smaller?
What if two spherical masses of reaggregated sponge cells adhered along one side?

A Simple Mistake Often Made in Biophysics:
Regarding tensor quantities as scalars; And also the reverse:
Regarding scalar variables as being capable of varying with direction.
The tension of a cell's cortex and plasma membrane is a second order tensor, and can therefore easily have different amounts in perpendicular directions; Tension can even be positive along one axis, but zero or negative in the perpendicular direction. A good example is that cytokinesis is caused by contractility of a ring of cell surface becoming very anisotropic. Contractility becomes much stronger in the circumferential direction than in the direction perpendicular to that, generally about twenty times stronger.

Nevertheless, very good scientists have used suction pipettes to measure "THE" tension in cell surfaces (as if there were only one tension, independent of direction). They measured how much suction force is needed to pull small predetermined volumes of cortex up into the tip of a micropipette. By this method, they get a single number. They also get praised for being more "quantitative" than most other researchers. But what do they measure? Some unknowably weighted average of the amounts of tensions in different directions. What if, at a specific location, there happens to be 10 units of tension (stress) in one axis, but only 2 units of stress in the perpendicular axis (at the exact same point). What will the suction pipette measure? Will it measure 10 units, or 2 units, or maybe their average, which is six units, or their sum (12 units)? The answer to these questions depends on the flexibility of the cortex, and would not be easy to measure. Furthermore, variations in flexibility (resistance to bending) would alter the apparent measures of tension. A less flexible area of cell surface would be interpreted as being under stronger tension.
Similar to the suction pipette method is the use of tiny microprobes to indent small areas of cell cortex by a set amount. The amount of pressure needed to produce some standard size dent is interpreted as measuring the strength of tension in the cell cortex. The possibility that this tension varies as a function of direction is ignored. Also being ignored is whatever amount of outward pressure contributes to the resistance to indentation. A single number is produced. This number is based on at least three independent variables: two tensions in perpendicular axes, some amount of outward pressure, plus some contribution from resistance to bending.
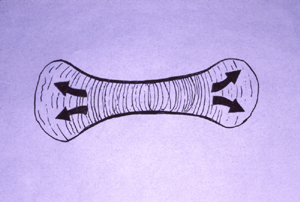
A reverse mistake is also often made by the best textbooks and researches. Osmotic and fluid pressures, although they are scalar variables incapable of varying with direction, are often thought to produce directional effects. Elongation (growth) of cartilages usually is attributed to directional secretion of sulfated polysaccharide matrix, especially chondroitin sulfate. Osmotic pressures and chemical concentrations can easily and often in one location as compared with another location. But they can't vary with direction. Neither a concentration nor a pressure within a liquid can be stronger in one direction than another. Therefore, the directional elongation of growing cartilages has to be attributed to directional differences in the resistance to swelling. This is directly comparable to inflation of an elongate balloon. The internal pressure is equally strong in all directions. The elongation of the balloon results from directional differences in the rubber layer's resistance to stretching.
Are there solutions to these difficulties, besides simply not falling prey to the fallacies (and avoiding excessive reverence for over-simplified "quantitation"? Specifically, can anyone devise methods that measure each directional component of tensile stress? For example, referring back to the postulated cell that had 10 units of tension in one axis and only 2 units of tension in the axis perpendicular to the first.
The goal we should seek would be determination of the exact directions in which there are ten units of tension, and also the directions in which there are two units of tension. To that information should be added the actual quantities of tension (ten and two) in those directions.