Biology 441, Spring 2013: Lecture notes, February 8
How many kinds of symmetry can you find in the picture below?

Symmetry is the best unifying concept for shape and pattern generation:
1) Human oocytes have an infinite number of planes of reflection symmetry.2) Developing embryo are reduced to just one plane of reflection symmetry..
3) This remaining symmetry is then "broken" , by a cellular mechanism which depends on the 9-fold rotational symmetry. of flagella.
4) Reduction of symmetry is called symmetry breaking,which is fundamental to development of animals (and plants), and sometimes is accomplished by gravity, locations of sperm entry or by amplification of random stimuli.
5) The segmentation of the spine, ribs and segmental nerves form displacement symmetry..
6) Driesch's. "embryonic regulation" includes at least 8-fold dilation symmetry..
7) Each kind of symmetry is defined by some geometric operation. (e.g. reflection, or rotation, or displacement, or dilation : which means magnification or shrinkage) which leaves an object looking the same as it did before.
8) Physical forces. and other causes also have particular symmetries.
9) Effects have the same symmetries as their causes ("Curie's Principle.").
10)
Laws of conservation of energy, momentum, electric charge etc. turn out to be results of
symmetries of physical forces and other laws. For every symmetry, a conservation law...
This amazing fact is called "Emmy Noether's Theorem.", but is Physics not Biology.

Lots of books have been written about how to apply symmetry to science.
Review: If twisting something leaves it looking the same as before...
Then we should say it has "twist symmetry."
For embryos to develop that symmetry, some force would have "twist symmetry".
If laws of nature had "twist symmetry", then there would be a law of conservation!
Please understand that there is no such thing as "twist symmetry"; It's just an example...
"There are more things in heaven and earth, Horatio, than are dreamt of in your Philosophy"
Shakespeare, Hamlet, Act One, Scene Five
For example: There are a lot more different kinds of symmetry, than just reflection symmetry. In fact there are more kinds of reflection symmetry than most people realize. Horatio didn't know!

Also, not just objects, but also forces have symmetries. Objects that are created by forces almost always have the same symmetry as the forces that cause them.
Soap bubbles have spherical symmetry because the air pressure inside pushes outward with the same force in every direction (Spherical Symmetry), ... and the tension in the soap film is also equal in strength in every direction.
Symmetries of crystals result from the symmetry of packing of molecules & ions.
The earth and the sun are spheres because the counterbalanced forces that shape them have the same strength in every direction. Notice that the forces are different in each of these cases: soap bubble, spherical balloon, earth, sun...
But forces that are equally strong in every direction (meaning they have spherical symmetry) cannot produce any shapes but spheres.
Please notice that oocytes of most species are spheres (Humans, birds, fish, sea urchins!
But not Flies (because their attachment to their "nurse cells" has only reflection symmetry).
Can you explain why human oocytes are spherical?
Even blastulas have almost spherical symmetry.
Axial Symmetry. (which many people call "Radial Symmetry", but I prefer not to) is what you call it when an infinite number of planes of symmetry intersect along a line. For example, an ordinary drinking glass, and unbent pipe or rod, all have "Axial Symmetry"
In order for something to become cubic in shape (like salt crystals) some force needs to have cubic symmetry (which is a certain combination of reflection symmetries). In salt crystals, this special symmetry is contributed by the packing of the ions.
Crystallographers have organized their subject primarily around symmetry concepts., and relating the macroscopic shapes of crystals to the combinations of symmetrical packing obeyed by their component molecules or ions.
What sort of cause is needed to convert a spherical oocyte to an axially symmetrical blastula?
"Symmetry of a cause is a subgroup of the symmetry of the effect, or corresponds to it." This is called "Curie's Principle", named after Madame Curie's husband.. Effects have the same combinations of symmetries as their causes (almost always) This applies to all sorts of things, including algebraic equations, and their graphed curves. Y = X squared, or to any even power, has a graph with a vertical plane of mirror image symmetry. That is because Y for any positive value of X has the same value as for the negative value of X. For equations like X=Y, in which x and y can be interchanged, then the graph has a diagonal plane of symmetry.
The equation X squared plus Y squared equals a constant gives a circle, because interchanging X with minus X, Y with minus Y, and X with Y all cause no change. From now on, you will be able to amaze your friends by knowing what symmetry the graph of an equation has to produce, won't you.
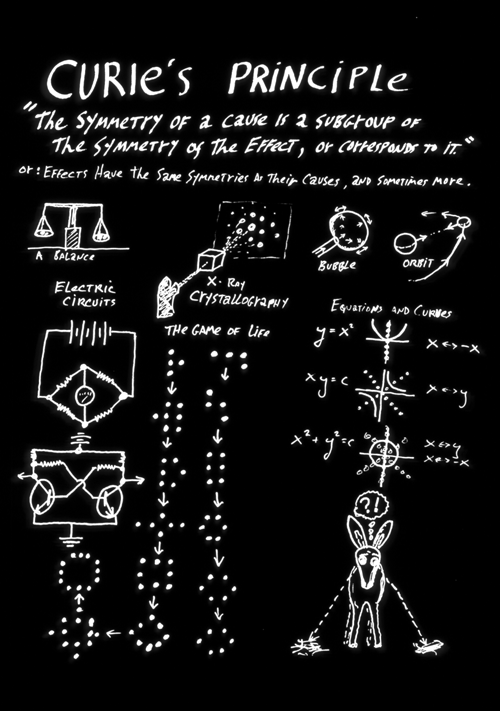
In X-ray Diffraction or in Electron Diffraction methods, the geometric patterns of spots produced is not a map of the submicroscopic molecules or ions in the crystal, but the diffraction pattern does have the same combination of symmetries.
The traditional style of weighing balance has mirror image symmetry for a reason.
In electronics, Wheatstone Bridges have two planes of symmetry for a reason.
Please don't panic if these things are not intuitively obvious.
Some medieval philosophers supposed that you could starve a donkey to death by putting it exactly half-way between two piles of hay. It is worth meditating on why this isn't true. Would it be true if hay repelled donkeys? Hint: maybe.
Also, the circuit diagram below the Wheatstone bridge is a classic transistor "flip-flop" that becomes stable when either of two electrical paths exist, and is the original memory device for computers.
Before we get back to embryos, I want to repeat some even more profound aspects of symmetry (which you won't be tested on in this course, but are pretty neat.)
______________________________________________________________________
Profound fact number one (That you won't be tested on)
"Emmy Noether's Theorem" which is named after a German woman mathematician who came as a refugee to the US and was a Professor at Bryn Mawr College, which is a Quaker women's college, about a dozen miles south-west of Philadelphia.The laws of conservation of momentum, angular momentum, electrical charge, energy & mass, and at least two others, are each based on a specific symmetry in laws of physics. If laws are unchanged by time displacement, then energy is conserved, etc. Symmetry with respect to quantum mechanical wave phase = conservation of charge.
Richard Feynman said, speaking very seriously, that Noether's Principle is the single most profound fact in all of physics.
______________________________________________________________________
Profound fact number two (That you also won't be tested on)
"Geometric Duality"In every (true) theorem of either Euclidian Plane Geometry, Solid Geometry, or Projective Geometry, you can interchange certain pairs of words (point <-> line) and produce another theorem which is its "Dual", and which is also true. A French mathematician discovered this, and proved it mathematically, in the early 1800s, which resulted in hundreds of new geometric theorems being discovered (automatically!)
http://en.wikipedia.org/wiki/Duality_(projective_geometry)
http://mathworld.wolfram.com/DualityPrinciple.html ______________________________________________________________________
Remember, you won't be tested on this, either.
A third amazing aspect of symmetry:
If you take any electronic circuit, and replace every capacitance by an inductance, and also do the reverse, replace every inductance by a capacitance, then the new electric circuit will behave the same way as the original circuit (if the original was an amplifier, then the new circuit will also be an amplifier; and so on for every possible function.)
____________________________________________________________________
NOW BACK TO STUFF THAT YOU WILL BE TESTED ON
The Mathematician-Physicist names Ernst Weyl defined all forms of symmetry by saying that if there is something you can do to an object (like reflect it in a mirror), and the object looks the same afterward as it did before, then the object has whatever kind of symmetry as the action that left it seemingly unchanged (in this case, reflection symmetry)
So, for example, if it looks the same after you rotate it by 180 degrees then it has two fold rotation symmetry; if it looks the same if you rotate it by 120 degrees, then it has three-fold rotation symmetry.
If it looks the same after you magnify or shrink it, then it has dilation symmetry.
Please notice that dilation symmetry is connected to Driesch's embryonic regulation.
If Driesch had known more mathematics, then he might have decided that his discovery proved that embryonic shape-generating mechanisms have dilation symmetry. (In species with regulative development, at least; maybe also in mosaic species)
For example, in Dictyostelium and other cellular slime molds, the mechanisms that cause formation of stalks and spore masses have a huge amount of dilation symmetry. These shape-creating mechanisms also have axial symmetry (because the shapes of the stalk and the spore mass both have axial symmetry).


Pyramid of the Sun and Pyramid of the Moon, Teotihuacan, Mexico
These pyramids have reflectional and dilation symmetry.
In applied mathematics, dilation symmetry is called "Scaling". This is in the sense of scale models, like scale model electric trains, scale model ships and airplanes, etc.
The best-studied example of scaling in physics is explosions and "Mushroom Shaped Clouds". Clouds produced by explosions will produce the same shaped clouds over a range from the size of a small terrorist bomb (10 pounds, 50 pounds, etc.) up to many megaton hydrogen bombs. When I was a graduate student, a right-wing group set off a bomb a block from our apartment; and what the books say is true; the cloud was only a couple hundred feet wide and tall, but looked like news photographs of nuclear bombs. Actual mushrooms (Fungi, like you see coming out of the ground) also "scale" over at least a ten-fold range. Much more biological research is needed on anatomical scaling.
Another big concept, related to symmetry, is stability:
Divergence away from a stable state: Can break symmetry.
Is achieved either by positive feed-back, or loss of negative feedback
Convergence toward a stable state: Can create shape, & create symmetry
Is best achieved by negative feed-back, homeostasis
How to "break symmetry"
In order to form an animal body, starting with a sphere (or from a disk) (Both of which have infinite numbers of planes of reflection symmetry)(e.g. oocyte stage for most kinds of animals; and continuing as late as the blastula stage or its equivalent for embryos of many kinds of animals, including humans)
-
some method is needed to "Break" symmetry.
-
[Very important! Somewhat difficult.]
B) and then causing the right and left halves to become anatomically different from each other, aorta goes toward left, etc.)
Those are two important example of breaking symmetry.
Most of the research on the former (A) happens to have been done using frog and salamander one-cell-stage embryos; also brown alga, kelp such as Fucus, 1-cell-stage.
(Although there are hundreds of other examples, only a few of which have been studied)
In Fucus, the root-leaf axis (which they call by another name, but same meaning) of a spherical cell can be created by light direction, pH gradients, voltage gradients, and a dozen or so other directional cues. For example, the future root sprouts on the darker side of the spherical one-cell stage, unless this directionality is somehow over-ruled by an electric field, or one of the other directional triggers. Many facts about this creation of oocyte directionality were discovered by Prof. Ralph Quatrano, who was chairman of this department for many years in the 1980 and 90s. This work was done during that time by him and one graduate student in particular, whose name deserves to be included here (& will be as soon as I find or remember it.)
In embryos of frogs and salamanders the plane of right-left reflection symmetry is selected from the infinite number of alternatives by the location where the sperm enters the oocyte. This location becomes what seems to me the anterior, but to most people seems like the dorsal, side. (This is not a disagreement about facts, just words, and so I recommend you get used to calling it the dorso-ventral axis, in case it turns up on Med School entrance exams). The grey crescent is caused to form 180 degees opposite to where the sperm enters; and that causes the blastopore to develop at or near the grey crescent.
As I mentioned previously: The direction of gravity can also create this breakage of symmetry. Centrifugation can also over-rule or superimpose itself on the symmetry symmetry-breaking of frog and salamander 1-cell stage embryos.
Please consider the analogy to a old-style punching-dummy in the drawing below. I had one of these things when I was about 4 years old; it helped me understand physics. Those dummies were (are?) made with an approximately hemispherical bottom, and with a metal weight at the bottom center.

When you punch the top part, the whole upper part rolls away from you, and then rolls right back. The reason is not difficult to visualize. Because the weight is below the center of curvature of the hemispherical bottom, pushing the dummy to any non-vertical angle has the effect of raising the weight slightly. Gravity therefore pulls the axis back toward the vertical orientation. I mean this to be an illustration of how a system can gravitate toward having some particular orientation, or any other property. The term asymptotic stability is used by mathematicians. The counter-balanced forces can perfectly well be weights, springs, motors, or muscles. Lots of people mistakenly equate this kind of stability to minimization of thermodynamic free energy (Which is a magical incantation to them; that they honestly believe.)
Next, visualize how the dummy's behavior would change if some kind of little internal elevator lifted the weight. As the weight approached the center of curvature, this would reduce how strongly the dummy would resist pushing, and how strongly it would gravitate back toward the vertical orientation.
If the weight were raised all the way to the center of curvature, this would eliminate the resistance to pushing, and also remove the tendency to roll back toward the vertical. It would behave like a basketball, with no more tendency for one side to be up, in preference to any other side being up. No stability.
Finally, what will happen if your small imaginary elevator lifts the weight above the center of curvature. That would make the dummy unstable. It would roll over in a random direction, and just lie there. If a fly had landed on one side, just at the moment when the weight rose past the center of curvature, then the dummy would have fallen toward the side with the extra weight (of the fly). Alternatively, if even a very weak wind had blown on the dummy, that tiny force would have become able to push the dummy over in the direction toward which the wind had blown.
The same result could be produced by the right kind of re-shaping of the curvature of the bottom, so that its center of curvature was shifted downward, below the weight. Please don't worry if you have trouble visualizing this; but give it a try. Standing up in a canoe is another good example of raising a center of weight above a center of (in that case) buoyancy.
What is the point of this punching dummy, and its change in behavior that changes so much depending on where the weight is relative to the center of curvature? It is meant to give you a mental framework for visualizing what sort of properties are needed to break symmetry.
Something in the oocyte or the embryo needs to reduce its stability toward neutrality, and then slightly beyond.
How should scientists try to understand symmetry breaking causes, like sperm entry, gravity, or the direction of flagellar waves? (which turns out to be the trigger for initiating right-left asymmetry in the human body, and probably all mammals and birds).
The usual perspective (of which the textbook is a good example) is to focus only on the movements in the cytoplasm, the redistribution of signal proteins (like Sonic Hedgehog), and particular genes whose mutation can cause failure of the system. (including "Lefty" and any of a long series of genes that code for component proteins of flagella.
Please do not interpret the next question as sarcasm: Please consider whether a molecular perspective is equivalent to trying to understand why the punching dummy fell over spontaneously by finding out what kind of plastic the dummy is made of, and whether the weight is made of lead or iron? (Likewise, in the case of not standing up in a canoe, is the key question whether the canoe is made of wood, aluminum or plastic? Or is the most important question the height of the person standing up?
My point is that it is at least as important to ask:
* Why the parts of the embryo were previously stable?
** What changed to destroy this stability?
*** And some other causal questions, too? Please suggest some.
Serious attempts to pose these questions in answerable forms were made by C. H. Waddington and Rene Thom and others during the 1960-70s and later. (Including several great Russian mathematicians: of these, Vladimir I. Arnold died recently. This approach was at the heart of what Thom called "Catastrophe Theory", (in the sense of abstract analysis of what makes systems undergo large-scale spontaneous changes). All big self-caused jumps in geometry or any property were called "catastrophes". Not enough research scientists had the patience to follow the logic. The approach wasn't disproved, or anything like that; It just didn't make enough useful or unexpected predictions to keep enough people interested.
I can tell you from experience, my only success getting most scientists follow a complex line of reasoning is to produce dramatic and unexpected photographs or time lapse videos that shake the out of their habitual assumptions.
It isn't enough to tell Horatio that there are more things in Heaven and Earth, you also need polaroid photos of the Ghost.
Otherwise people not only prefer to analyze what kind of wood canoes need to be made of in order to turn over, which makes them proud of being more "practical' and "molecular".
web sites about symmetry:
http://mathworld.wolfram.com/DualityPrinciple.htmlThis is an intelligent and accurate web site about many applications of symmetry (even to music!). You are not assigned to read it, but it could help you understand the topics covered in lecture and on the course web site.
The subject of symmetry is very wide and deep - like the Grand Canyon. So take a few minutes to look down into its beautiful depths, and even spend five or ten minutes hiking down in there to expose your mind to more profound concepts. Personally, I have been lucky enough to climb quite far. In additional to the conceptual beauty, you can take pleasure in the fact that you definitely won't need to know so much on exams in this course. We definitely are dealing with true profundity here, not pseudo-wisdom.
But if you have plenty of extra time and more brains than you know what to do with, try these:
http://en.wikipedia.org/wiki/Fractal
http://en.wikipedia.org/wiki/Circuit_theory-
http://en.wikipedia.org/wiki/Noether%27s_theorem
These are all completely accurate, as far as I can tell. Also well explained.
A major embryological question is "How do embryos manage to become less symmetrical " Break Symmetry" but avoid becoming random.
Sometimes symmetry breaking is accomplished by external stimuli.:
A good example is that the anterior-posterior (most people say dorso-ventral)body axis of frog and salamander embryos isstimulated to form by the location where the sperm enters. the egg cell at fertilization. You should learn dorso-ventral. This isn't a dispute about facts, but a preference in how to visualize things.
Whichever side the sperm enters is thereby caused to develop into the rear end.of the future frog or salamander.
Until then, the oocyte had an infinite number of planes of mirror-image symmetry, all intersecting along a straight line that runs between the animal pole and the vegetal pole.
Sperm entry triggers a massive, activecortical rotation of thelayers of oocyte cytoplasm oocyte cortex relative to the deeper underlying cytoplasm, and in some species a "Grey Crescent." forms on the opposite side, below the equator. This area is visibly grey in color only in some species, but always has special properties. One very clever way to studycortical rotation is to apply spots of two different fluorescent dyes, one of which binds to molecules on the surface, and the other of which diffuses down into the deeper cytoplasm. The spots of surface-bound dyes slide dramatically past the spots of dye that have diffused down into deep cytoplasm. I really envy and admire the inventor of this experiment. We should draw a diagram of how it works. Or maybe draw an animation!
The location of sperm entry also controls the anterior-posterior axis of nematode worms. This was discovered by Prof. Goldstein of the UNC Biology Department!
What would you predict would happen if frog oocytes were fertilized exactly at their animal poles? In other words, what if no directionality were provided by the location of sperm entry?
One possibility: A very abnormal tadpole would develop which is either all mouth or all tail, 360 degrees around its periphery, or in some other way retains all of its million planes of reflection symmetry?
Another possibility: Another, unknown, or random disturbance would trigger a cortical rotation that is indistinguishable from cortical rotations that are stimulated by sperm entry.
This reminds me of a joke about some change being so hyper-sensitive that it will occur "not only at the drop of a hat, but in the presence of a loosely-held hat"
This degree of hypersensitivity runs the risk that two different body axes will be stimulated to form, in the same oocyte. (conjoined twins). This can be caused to occur simply by holding a recently-fertilized frog oocyte upside down (animal pole down). The higher density and weight of the vegetal pole cytoplasm shifts downward and this causes formation of two grey crescents, and thus two separate blastopores on opposite sides of the embryo. This was originally discovered in the 1890s, and then re-discovered in the 1980s.