Do hypothetical gradients really exist? What evidence supports which theory? __________________________________________________________________
Although I have published papers about some of the theories discussed here, I promise not to try to "sell" them, & won't give better grades for exam answers that support those particular theories. Arguments against them will get better grades.
___________________________________________________________________

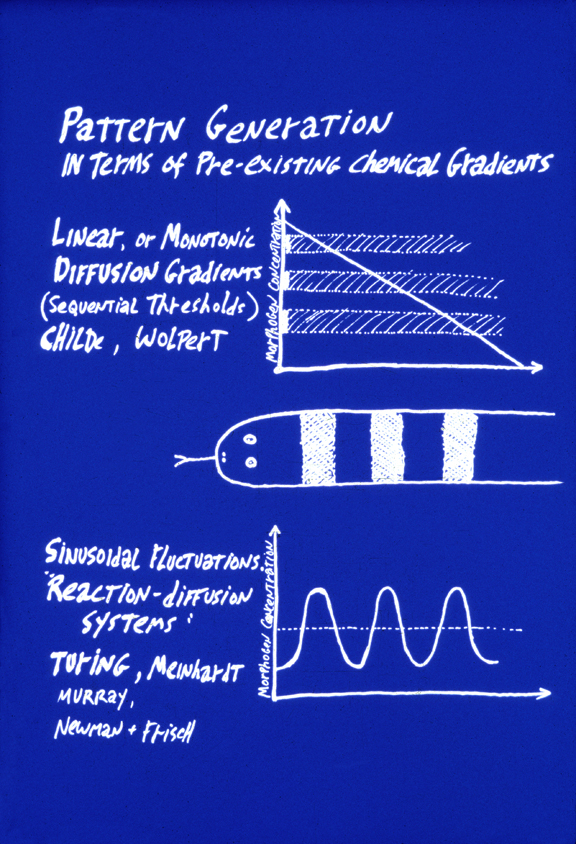
The important distinction between "Prepatterns" versus "Positional Information”.
Each of these are families of related theories.

QUESTIONS FOR CLASS DISCUSSION:

a) Turing's mechanism is which: a prepattern theory, or a positional information theory?
Hint: A prepattern theory. Because the geometry of the biological pattern is the same as that of the signals that cause the pattern.

b) What about Liesegang rings?
Hint: They are a category of chemical reactions that actually create lines and spots, by mechanisms that might also occur in the body, except probably not using salts.

c) Do embryological prepatterns have to be wave-like?
Hint: not at all. Waves are easier to think about. Also many biological patterns do have repeating spatial features.

This is a photograph of an actual snake (A juvenile Black Rat Snake).
Please look carefully at its color pattern, both regularities and irregularities.
Try to find evidence for causal mechanisms.

Do widths of bands become smaller where the snake's body is narrower?

Do boundaries of spots tend to align with boundaries between scales?

Are light colored areas lightest next to dark areas?
Are darker areas darkest next to light areas?

QUESTION d) What would you conclude if a "Turing-like" theory predicted some of these regularities?

This is a photograph of that same snake seen from below

QUESTION e) Please find at least two phenomena that you would probably not have guessed.
Hint: gradient & stripes

Incidentally: If you ever get bitten by any snake, even if non-poisonous, make sure you have, or have recently had, a tetanus vaccination. Even a non-poisonous snake-bite is a puncture wound.

Photograph of a copperhead snake.

QUESTION f) What regularities, and what irregularities do you notice?

Are light colored areas lightest next to dark areas?
Are darker areas darkest next to light areas?

Some more snake patterns:

Trans-Pecos Copperhead.

Trans-Pecos Ratsnake

California King Snake

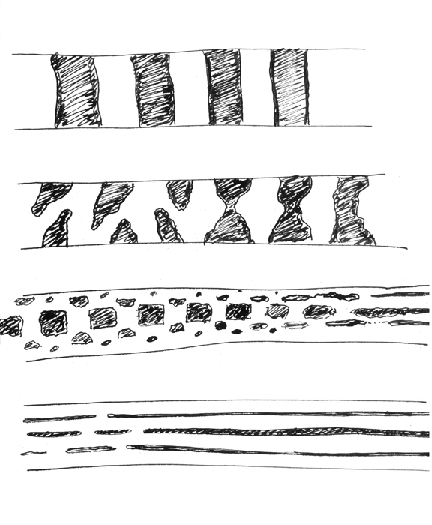
If you look through books about snakes, you find examples of these color patterns. Sometimes one part of a snake's body will have longitudinal stripes and another part of that same snake's body will have circumferential bands. Stripes tend to be near the head on the top.

The California King Snake color patterns are interesting because some individuals have stripes and others have bands. This is a one-gene difference. The subspecies of King Snake that we have in the eastern US has white hexagons on a black background. Other regional variants have very small black and white speckles ("Salt and Pepper" pattern)

Some embryologists have tried to write computer programs that generate these same variations that occur in the color patterns of actual snakes (and NOT patterns that don't occur in snakes). For example, lateral inhibition creates darker edges of dark spots. Another key idea is that realistically snake-like irregularities should be generated by small amounts of randomness in some of the variables of such computer programs. (Examples of "snake-like irregularities" are those dark bands that fail to connect across the back, but instead swerve away from each other, as if somehow repelled or inhibited.

QUESTION g) Figure out how a pattern-generating computer program can be switched from producing stripes to producing bands.
Hint: Some clouds elongate parallel to the wind ("Wind Streets"), but other clouds elongate perpendicular to the wind. What pattern is intermediate between these two extremes?

Cloud "streets" (Convective rolls over mid-Atlantic)
(Hurricane Gabrielle, I think.)

QUESTION h) How can embryologists prove whether or not actual anatomical patterns are produced by mechanisms that are logically equivalent to the one that Turing hypothesized?

Two diffusing chemicals; one stimulates and the other inhibits; the inhibitory one diffuses faster.

http://www.wired.com/2011/02/turing-patterns

"That markings on animals are produced by Turing systems of pigments is now generally accepted, but the origin of what appear to be Turing patterns in more complex settings — such as limb and tooth and lung development — is still debated.

A basic step towards proving the existence of these three-dimensional Turing patterns is demonstrating a three-dimensional pattern in the lab. In a paper published Feb. 11 in Science, researchers led by Brandeis University chemist Irving Epstein do precisely this.

The researchers set off a chemical reaction that creates Turing patterns in laboratory flasks, then used tomography — a form of imaging used to reconstruct three-dimensional images from thousands of two- dimensional snapshots — to picture them.

"It's an intellectual coup," said Epstein."

    (Quoted from an article in Wired magazine, the URL for which is written above).

QUESTION i) Please argue pro or con, supporting or contradicting that quote from Irving Epstein.

QUESTION j) Can Turing's method for generating chemical concentration patterns produce the phenomenon discovered by Driesch? In other words, if an embryo is made smaller, will the chemical waves form closer together?
Hint: Not unless the diffusion rates or reaction rates change in proportional to the size of the embryo. (Which isn't totally impossible, but why would such an ability have evolved, unless somehow intrinsic.)

Some species of fish have wide stripes alternating with narrow stripes. This is supposed to be caused by the larger stripes being formed by a Turing mechanism when the fish was small. Then the narrow bands form by the same Turing mechanism when the fish gets bigger.

____________________________________________________________________________________

An extremely different category of pattern-generating method:

a) Three or more linear diffusion gradients form, each perpendicular to the other two.

b) Each cell measures the three concentrations at its location of these three "morphogen" chemicals.

c) An unspecified molecular mechanism "interprets" the combination of three morphogen concentrations.
(For example, if concentration #1 were 22% maximum, and #2 were 55% maximum and #2 were 77% maximum. then the unspecified interpretation could be "differentiate into a chondrocyte".

PLEASE NOTICE:

* The key idea is that diffusion gradients should be twice as steep in half-sized embryos, ten times as steep in tenth-sized embryos, half as steep in double-sized embryos.

** The chemical morphogens of positional information are very different that what Turing invented that word to mean.

*** The spatial variation of morphogen concentrations does not form any geometric pattern
(other than linear, or at least monotonic gradients).

**** Most developmental biology textbooks do not distinguish between these uses of the word "morphogen".

The following paper is not assigned, but in case you are interested in what some big shots are thinking, you might take a look at it:

http://www.pnas.org/content/110/41/16301.full

A quotation from that paper: "In a developing embryo, individual cells need to "know” where they are to do the right thing. How much do they know, and where is this knowledge written down? Here, we show that these questions can be made mathematically precise.

Notice the irony of explaining size regulation using observations on species (flies) with mosaic development.

________________________________________________________________________________

QUESTION k)
Below is a quote from the "Biology Online" definition of positional information

"The instructions that are interpreted by cells to determine their differentiation in respect of their position relative to other parts of the organism, for example digit formation in the limb bud of vertebrates.

Discuss hidden, unstated assumptions of this definition.

To begin, does it assume embryos develop by Wolpert's method or by Turing's method?

Understand that Turing's hypothetical Reaction-Diffusion system, Liesegang rings, (and all other reaction-diffusion systems) are methods of producing prepatterns.

Ironically, if you Google "Positional Information" you find articles about prepatterns.

http://en.wikipedia.org/wiki/Pattern_formation

http://www.cc.gatech.edu/~turk/reaction_diffusion/reaction_diffusion.html

(Greg Turk did his PhD at UNC in the Computer Science Department, although one of the 5 members of his thesis committee was a Biology Professor.)

_______________________________________________________________________________________

Other hypotheses, that are in competition with Turing's and Wolpert's

"Biomechanical" methods: instead of cells responding to chemical concentrations, cell movements and force exertion can directly generate anatomical patterns.

For example, stripes on zebra-fish may result from cell-cell attraction and/or repulsion. This also needs computer simulation.

Tensegrity: a widely popular set of ideas that cell shapes and arrangements result from counter-balances between tensions and pressures. Donald Ingber has written the best papers on this subject.

The Differential Adhesion Hypothesis: Cells rearrange so as to maximize "work of adhesion" and minimize thermodynamic free energy; a theory invented to explain sorting out of randomly intermixed cells using different amounts of only one cell-cell adhesion protein, but which still has many supporters.

Shape Homeostasis: My own favorite invention. Similar to tensegrity, and based on cell forces changing strength in response to their current shapes and arrangements. Also based on analogies to thermodynamics, in the sense of convergent balances of forces producing the same effects as minimization of free energy (or as minimizing potential energy) but not literally minimizing any kind of energy.