Lecture notes for Wednesday, February 15, 2017   Symmetry in relation to Embryology: Not just descriptive, but also causal. Not just relevant to past discoveries, But a strategy for making future discoveries of your own. Not just a set of facts, but a perspective by which to make sense of shapes and shape changes. ********************************************** Sperm entry location -> plane of reflection symmetry in amphibia      ("grey crescent") Fucus - a kind of brown algae. Egg cell has spherical symmetry that changes to axial symmetry. This change can be triggered by many different environmental cues.   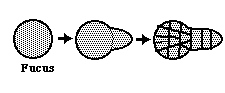Kartagener's Syndrome Male infertility and respiratory problems due to defective cilia. In 50% of people with this syndrome the positions of internal organs (aorta, pancreas, liver etc.) are reversed from their usual arrangement. Flagellar bending controls left vs. right: Rotation in flagellated cells in Hensen's node in the primitive streak determines the asymmetry of these organs in normal development (aorta is on the left side of the heart, liver is on the right). In Kartagener's syndrome, these flagellated cells are defective, and internal asymmetry is random.     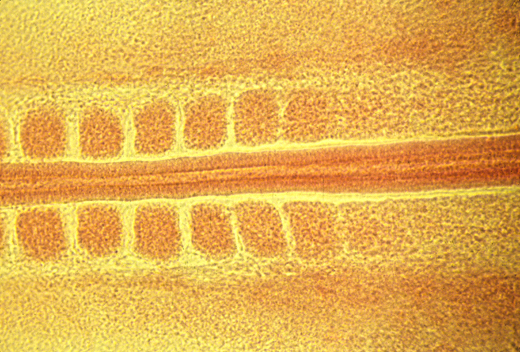Breaking displacement symmetry Somite formation: breaks anterior-posterior displacement symmetry. The "Clock and Wave-Front" theory is an attempt to explain this, and will be discussed further in another lecture. <- anterior                                            posterior ->     REACTION-DIFFUSION SYSTEMS: Turing's & other reaction-diffusion systems          "break" displacement symmetry. Turing's mechanism: Please memorize these three simple rules. (Although these are not the only rules that can produce patterns, and they are not even the same as the rules Turing proposed, they are a good example of how simple the rules can be. rule# 1) The concentration of chemical "A" causes more "A" and also more of chemical "B" to be produced. (= Synthesized? Activated? Released from vesicles? Anything!) rule# 2) Both "A" and "B" are destroyed (=Inactivated? Reabsorbed? Anything!) in proportion to the concentration of "B" at any location. rule# 3) "B"diffuses faster than "A" (Or in any way produces effects at longer range than A) The result of obeying these rules is formation of alternating waves of high and low concentration of both A and B. The peaks of A are a little higher than the peaks of B, but the B peaks are wider. Faster diffusion, and lower peaks result from faster diffusion. The peaks of A and B form at the same locations. You can generate alternating waves by using different sets of rules. The wave-length increase in proportion to the ratio of diffusion rates, and also changes if A or B reaction rates are changed. These rules will generate evenly spaced waves, either when initiated by Brownian motion of the chemicals, or by local differences in concentrations of A or B, or other perturbations. In two dimensions these rules will generate peaks or waves (depending on how you initiate them) In three dimensions, they generate regularly-spaced blobs of higher concentrations of A and B. Textbooks tend to assume only irregular patterns can be produced when randomness is used to initiate the process. Computer simulations show this is not true. (A certain textbook has a graph showing the supposed irregularity.) Another widely-believed fallacy is that B has to diffuse a lot faster than A. (Twice as fast can be enough, which is good because 5 or ten-fold differences in diffusion rates are difficult to produce with molecules whose sizes are in the same ball-park.) video with narration showing a pascal program with these rules. This was shown in class without the narration. Please watch the whole thing again with the sound.       LIESEGANG RINGS = "Liesegang Bands" Another kind of Reaction Diffusion System. discovered by accident, actually occurring in chemical reactions but not yet discovered in embryos or animals or plants (And the mechanism of which is not yet known for sure!!) (After a century of intensive research, and ~ 4,000 published research papers!) Dissolve a low concentration of potassium bichromate in water; also dissolve 2 or 3% by weight of gelatin in this same water. (Be careful: bichromate ion is a serious cumulative poison, NEVER touch it! If by accident you do; then wash vigorously.) Heat the water until the gelatin dissolves. Pour this solution into a thin (millimeter) layer in a Petri dish, and let it gel. Later, scatter a few crystals of silver nitrate on a small part of this gelatin surface. Instead of forming solid blobs of insoluble silver bichromate, what happens instead is formation of many concentric rings of precipitated silver bichromate, with clear gaps between the rings of precipitate. These gaps are what is unexpected and unexplained. Also surprising is that rings don't form if you dissolve silver nitrate in a gelatin solution, let it gel in thin layers, and then scatter crystals of potassium bichromate on top of that. That is some kind of asymmetry. However, rings do form if you put a small bichromate crystal on top of an area of bichromate gelatin gel where silver bichromate crystals are already formed. The Wikipedia site on this subject is well done. By using high power microscopes to making time lapse videos of Liesegang rings I have discovered several new and very unexpected phenomena. Videos: time-lapse video of Liesegang reaction heavy bands of precipitated silver bichromate forming over about one hour several additional clips of Liesegang bands forming A piece of thread was soaked in silver nitrate and laid across the gelatin containing the bichromate Pascal program simulating the Liesegang reaction -------------------------------------------------------- Our original Pascal programs can be run only in "Mac Classic" (OS 9 and earlier). We would like very much to hire someone to rewrite these programs in JAVA, Python or some other language, in a form that can be run on current Macs and PCs. Please contact us if you would be willing to help us do this. ******************************************************* Things to think about: Nobody has yet proven that any particular spatial pattern of either animals or plants really uses the logical equivalent of this (or other) reaction-diffusion systems. How would you prove (or conclusively DIS-prove) that something like stripes on a Zebra, or on a Zebra Fish, are generated by a reaction-diffusion system? What if you mutated the gene that codes for the "Morphogen" chemical "A" or "B"? What would the phenotype of such a mutation be? Suppose you inserted the amino acid sequence for GFP (green fluorescent protein) into the gene for protein A, or B (even assuming proteins? What would happen if you isolated substance "A" or "B", and put drops of these substances on a developing embryo, where it was forming spots, or somites were splitting apart from each other? How would the spatial pattern be changed that would prove that the isolated chemical really functions like "A" or "B". Suppose that you somehow knew for sure that chemicals A and B were among 10 or 20 chemicals that someone had isolated from body fluids of some kind of embryo; please design an experiment by which you could prove which of the purified chemicals is "A" and which is "B". Next, suppose that an embryo forms regularly-spaced spots. Can we invent a method for extracting substances "A" or "B". By that I mean, to extract them before you know what chemical they are. NOTE: Auxin was purified from oats before it was known for sure to exist. Serotonin was purified from blood when its existence was still hypothetical. Shouldn't hypotheses include experimental criteria for detecting, not just whether they are capable (in principle) of producing a given effect, but also testing where and when and whether that category of mechanism is going on? Not just a litmus test for acidity, but also a litmus test for "morphogen" chemicals, and even a litmus test for whether a reaction-diffusion is or is not the cause of some particular breaking of displacement symmetry.   Please graph concentrations of "A" on the x axis, and graph concentrations of "B" on the y axis, and for a few dozen points in A, B space, please graph little vector-like arrows that illustrate the changes on local concentrations of "A" and "B" as a result of their effects on their own and the other one's concentrations. For example, the arrows in the lower right (corresponding to A being more concentrated than B) therefore point diagonally upward and further to the right. That's because concentrations of both A and B would increase there. Conversely, the arrows in the upper left would point diagonally downward and back further to the left. A diagonal band of very short or zero-length arrows would slope upward and rightward from the point that represents A and B being zero. Such graphical representations of the net effects of combinations of equations are called "phase planes". By using phase planes, your brain can learn to recognize what net effects would be produced by any arbitrary combinations of equations. Phase planes can also be used to do the reverse, which is to invent combinations of equations that will, acting in combination, produce any desired combination of net effects. Incidentally, only those combinations of chemical reactions that produce diagonal boundaries between zones where arrows are pointed in opposite directions parallel to boundary. Can you invent "rules" whose phase plane representation will have a diagonal boundary running from upper left down to lower right, with the arrows above this boundary pointing parallel to this boundary, and in opposite directions on one side of the border as compared with the other side of the border. With effort, you can gradually become able to visualize what a phase plane has to look like in order to be able to break displacement symmetry. An impressive but (I think) misleading article about Turing's theory is at the following URL http://rsfs.royalsocietypublishing.org/content/2/4/487 You are NOT assigned to read it. It is long and designed to impress instead of to be understood, or to help you understand.