Lecture notes for Wednesday, February 14, 2018   Instabilities that Create Geometric Patterns Somite formation: breaking displacement symmetry <- anterior                                            posterior -> Sequential formation of somites from anterior to posterior in a chick embryo     CLOCK and WAVEFRONT HYPOTHESIS: The "Clock-and-Wavefront Hypothesis" was invented by Cooke and Zeeman to explain somite formation, and especially the ability of embryos to adjust somite size in proportion to the amount of paraxial mesoderm to be subdivided (If you surgically remove tissue, then smaller somites are made). The theory is/was that one quantity oscillates higher and lower in amount, while another variable forms a gradient that gradually increases in amount along its length. A somite is supposed to be split off each time the oscillator increases. Molecules (mostly proteins) have been discovered to behave as the theory predicted. But there are surprises! Three gradients have been found: Fibroblast Growth Factor, Wnt and Retinoic acid (the RA gradient running in the opposite direction [anterior high to posterior low] to the others). Fish use different "clock" substances than birds & mammals (Notch protein) Arthropods also use clocks & wavefronts; which wasn't expected.   REACTION-DIFFUSION SYSTEMS: Turing's & other reaction-diffusion systems "break" displacement symmetry. video with narration showing a pascal program with these rules. This was shown in class without the narration. Please watch the whole thing again with the sound.   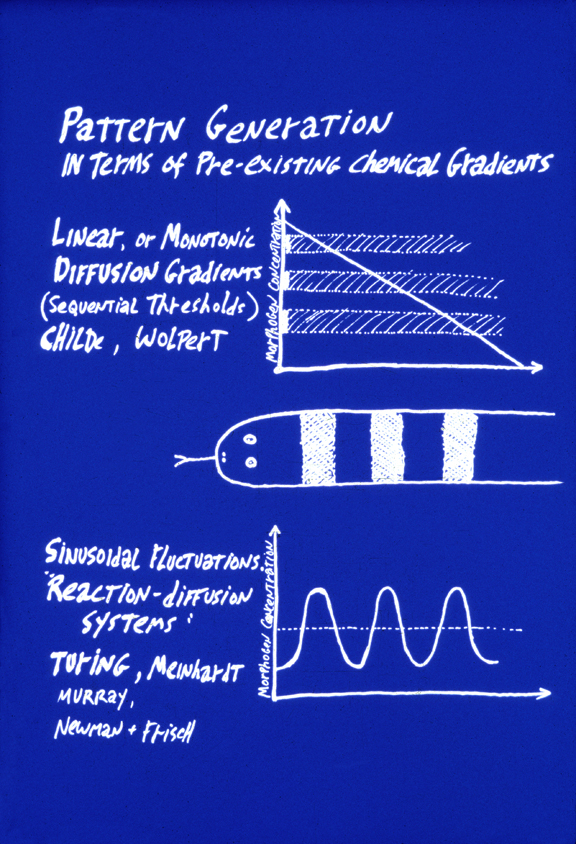CONTRAST REACTION-DIFFUSION WITH POSITIONAL INFORMATION:   The top of this figure represents the theory of "Positional Information" This concept was invented by Lewis Wolpert, specifically as a way to explain the Driesch phenomenon. e.g. separated 2 cell stage echinoderms developing into half-size larvae, and all that. a) Three or more linear diffusion gradients form, each perpendicular to the other two. b) Each cell measures the three concentrations at its location of these three "morphogen" chemicals. c) An unspecified molecular mechanism "interprets" the combination of three morphogen concentrations. (For example, if concentration #1 were 22% maximum, and #2 were 55% maximum and #2 were 77% maximum. then the unspecified interpretation could be "differentiate into a chondrocyte". The key idea is that diffusion gradients should be twice as steep in half-sized embryos, ten times as steep in tenth-sized embryos, half as steep in double-sized embryos.   Alan Turing's reaction-diffusion system is an alternative way to generate the same striping pattern. In this case, the concentration of some substance (also called a morphogen) varies along the length of the animal in a regular manner, creating a "pre-pattern" for the eventual stripes in the animal. " ** The chemical morphogens of positional information are very different that what Turing invented that word to mean. *** The spatial variation of morphogen concentrations does not form any geometric pattern (other than linear, or at least monotonic gradients). **** Most developmental biology textbooks do not distinguish between these uses of the word "morphogen". Sometimes they mean one definition, sometimes they mean the other!   Rules for Turing's mechanism: Please memorize these three simple rules. (Although these are not the only rules that can produce patterns, and they are not even the same as the rules Turing proposed, they are a good example of how simple the rules can be. rule# 1) The concentration of chemical "A" causes more "A" and also more of chemical "B" to be produced. (= Synthesized? Activated? Released from vesicles? Anything!) rule# 2) Both "A" and "B" are destroyed (=Inactivated? Reabsorbed? Anything!) in proportion to the concentration of "B" at any location. rule# 3) "B"diffuses faster than "A" (Or in any way produces effects at longer range than A) The result of obeying these rules is formation of alternating waves of high and low concentration of both A and B. The peaks of A are a little higher than the peaks of B, but the B peaks are wider. Faster diffusion, and lower peaks result from faster diffusion. The peaks of A and B form at the same locations. You can generate alternating waves by using different sets of rules. The wave-length increase in proportion to the ratio of diffusion rates, and also changes if A or B reaction rates are changed. These rules will generate evenly spaced waves, either when initiated by Brownian motion of the chemicals, or by local differences in concentrations of A or B, or other perturbations. In two dimensions these rules will generate peaks or waves (depending on how you initiate them) In three dimensions, they generate regularly-spaced blobs of higher concentrations of A and B. Textbooks tend to assume only irregular patterns can be produced when randomness is used to initiate the process. Computer simulations show this is not true. (A certain textbook has a graph showing the supposed irregularity.) Another widely-believed fallacy is that B has to diffuse a lot faster than A. 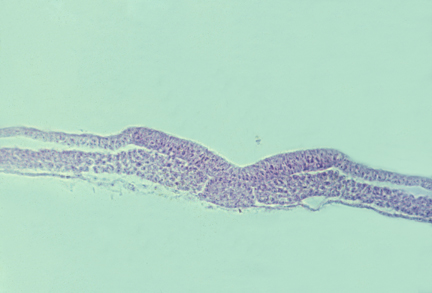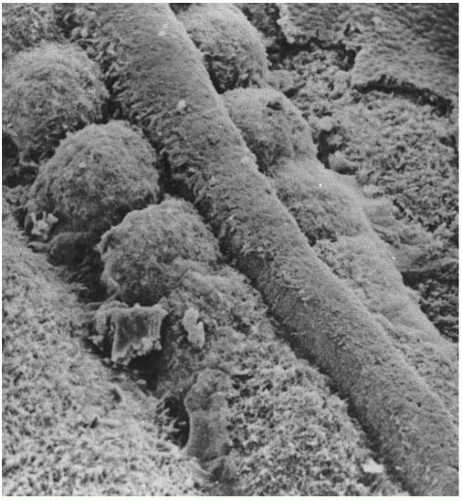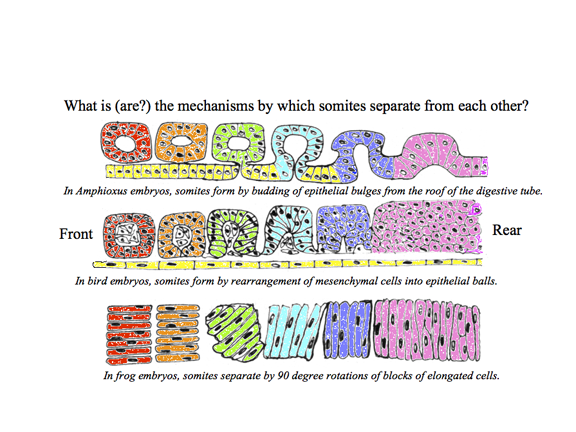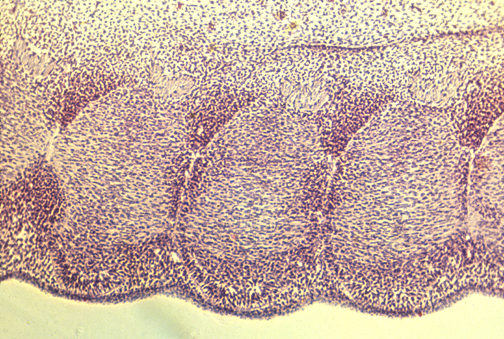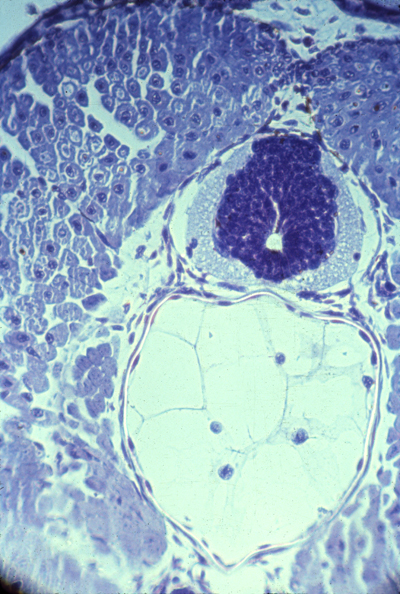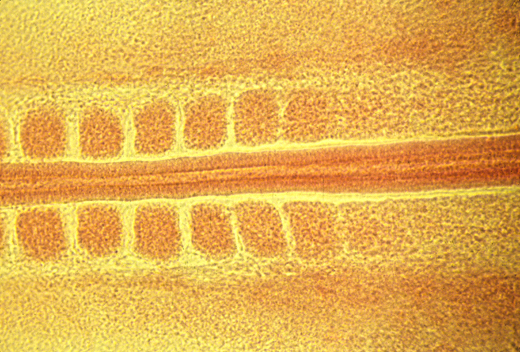(Twice as fast can be enough, which is good because 5 or ten-fold differences in diffusion rates are difficult to produce with molecules whose sizes are in the same ball-park.)   Somites and Notochord   cross-section of an amphibian embryo showing the neural tube (dark) and below it, the notochord, with vacuolated cells   longitudinal section of a salamander notochord   early neurulation in a chick embryo   scanning electron microscope image of chick embryo somites; by Kathryn Tosney     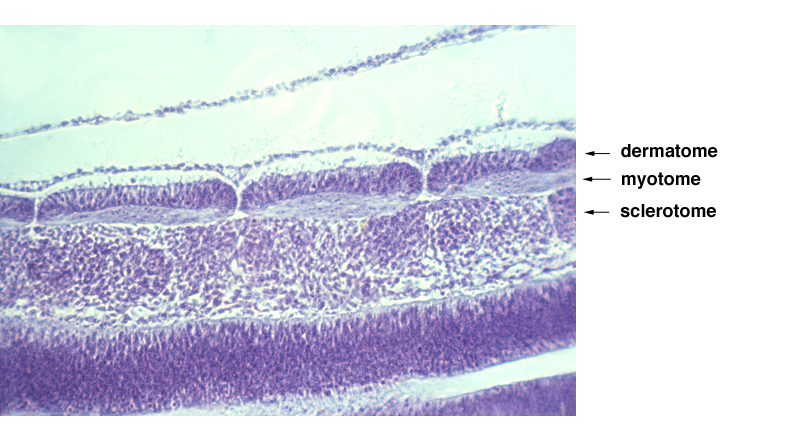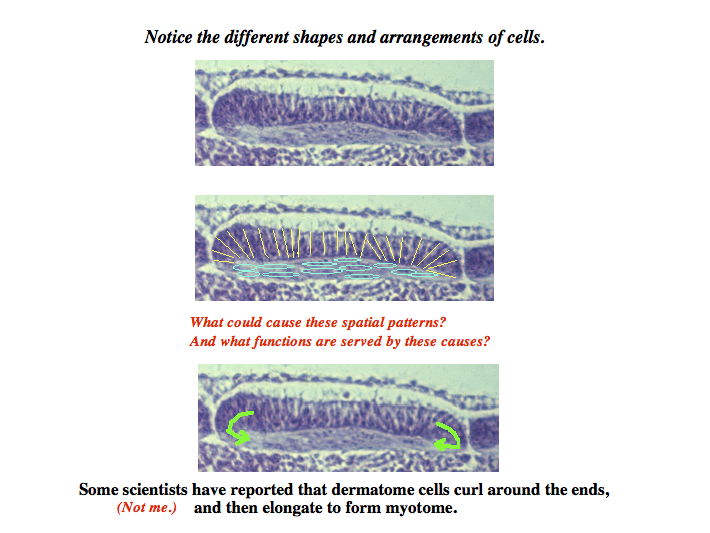subdivisions of somites: dermatome becomes skin, myotome becomes muscles, sclerotome becomes vertebrae   myotome formation   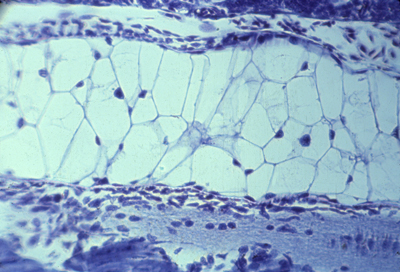section of myotome