Lecture notes for Friday, February 15, 2019   More on Symmetry Some videos showing cellular automata: Preservation of symmetry in systems that obey simple rules Cellular automata videos with different symmetries. 2-fold rotational symmetry 4-fold diagonal reflection symmetry 4-fold reflection symmetry(this is the one that was shown in class) 4-fold rotational symmetry This one has music More about how these programs work The simulations above are video recordings of runs of a Java program, created by a former student, that used to be accessible on this web site. Unfortunately the program no longer works because of security issues with recent computers. We would be most grateful for someone who could help us get around this problem, either by figuring out a way to bypass the security problems, or alternatively to rewrite the programs in some other format (Python? Swift? XCODE?) that could be downloaded and run on personal computers, iPads etc. without necessarily being connected to the internet. Some links to web pages on cellular automata (optional) Wolfram page on cellular automata a one-dimensional program in which you can choose the settings       Breaking Symmetry Becoming less symmetrical, without becoming irregular or random. That is the big problem. Human oocytes have an infinite number of planes of reflection symmetry Developing embryos are reduced to just one plane of reflection symmetry This remaining symmetry is then "broken" , by a cellular mechanism which depends on the 9-fold rotational symmetry of flagella. Kartagener's syndrome    a human genetic abnormality 1) Male sterility 2) More respiratory illness, accumulation of mucus 3) Half have situs inversus viscerum, i.e. reversal of the usual position of the aorta, pancreas, intestinal bending etc.    (about a tenth of people with this syndrome have partial right left reversal) The explanation is that right-left asymmetry is normally determined by the direction of beating of flagella in cells in Hensen's node.     Breaking displacement symmetry Somite formation: breaks anterior-posterior displacement symmetry. 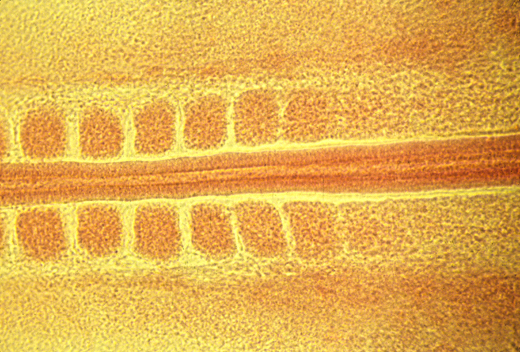<- anterior                                                                                         posterior ->     CLOCK and WAVEFRONT HYPOTHESIS: The "Clock-and-Wavefront Hypothesis" was invented by Cooke and Zeeman to explain somite formation, and especially the ability of embryos to adjust somite size in proportion to the amount of paraxial mesoderm to be subdivided (If you surgically remove tissue, then smaller somites are made). The theory is/was that one quantity oscillates higher and lower in amount, while another variable forms a gradient that gradually increases in amount along its length. A somite is supposed to be split off each time the oscillator increases. Molecules (mostly proteins) have been discovered to behave as the theory predicted. But there are surprises! Three gradients have been found: Fibroblast Growth Factor, Wnt and Retinoic acid (the RA gradient running in the opposite direction [anterior high to posterior low] to the others). Fish use different "clock" substances than birds & mammals (Notch protein). Arthropods also use clocks & wavefronts; which wasn't expected.   REACTION-DIFFUSION SYSTEMS: Turing's & other reaction-diffusion systems "break" displacement symmetry. Rules for Turing's mechanism: Please memorize these three simple rules. (Although these are not the only rules that can produce patterns, and they are not even the same as the rules Turing proposed, they are a good example of how simple the rules can be. rule# 1) The concentration of chemical "A" causes more "A" and also more of chemical "B" to be produced. (= Synthesized? Activated? Released from vesicles? Anything!) rule# 2) Both "A" and "B" are destroyed (=Inactivated? Reabsorbed? Anything!) in proportion to the concentration of "B" at any location. rule# 3) "B"diffuses faster than "A" (Or in any way produces effects at longer range than A) video with narration showing a pascal program with these rules. Please watch this again, pausing occasionally to see the changing values of the diffusion ratio at the top left. The result of obeying these rules is formation of alternating waves of high and low concentration of both A and B. The peaks of A are a little higher than the peaks of B, but the B peaks are wider. Faster diffusion, and lower peaks result from faster diffusion. The peaks of A and B form at the same locations. You can generate alternating waves by using different sets of rules. The wave-length increase in proportion to the ratio of diffusion rates, and also changes if A or B reaction rates are changed. These rules will generate evenly spaced waves, either when initiated by Brownian motion of the chemicals, or by local differences in concentrations of A or B, or other perturbations. In two dimensions these rules will generate peaks or waves (depending on how you initiate them) In three dimensions, they generate regularly-spaced blobs of higher concentrations of A and B. Textbooks tend to assume only irregular patterns can be produced when randomness is used to initiate the process. Computer simulations show this is not true. (A certain textbook has a graph showing the supposed irregularity.) Another widely-believed fallacy is that B has to diffuse a lot faster than A. 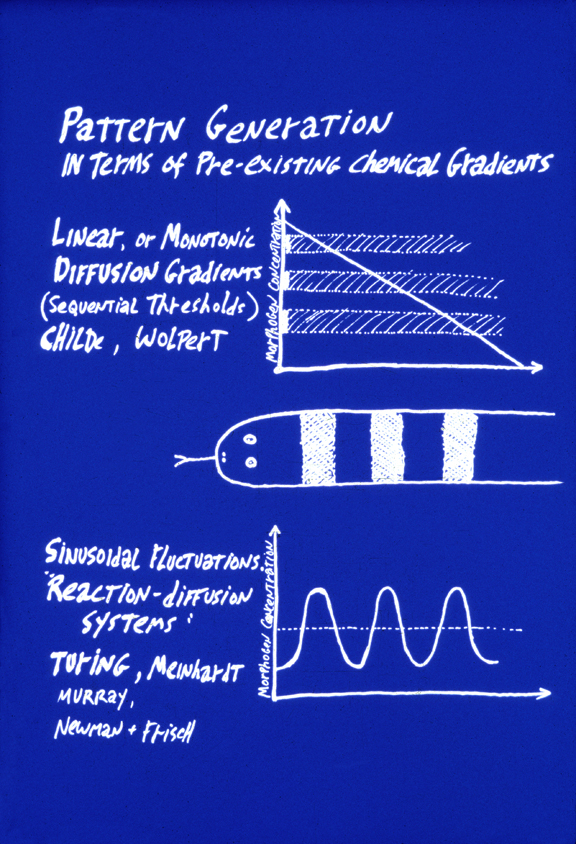(Twice as fast can be enough, which is good because 5 or ten-fold differences in diffusion rates are difficult to produce with molecules whose sizes are in the same ball-park.)   CONTRAST REACTION-DIFFUSION WITH POSITIONAL INFORMATION:   The top of this figure represents the theory of "Positional Information" This concept was invented by Lewis Wolpert, specifically as a way to explain the Driesch phenomenon. e.g. separated 2 cell stage echinoderms developing into half-size larvae, and all that. a) Three or more linear diffusion gradients form, each perpendicular to the other two. b) Each cell measures the three concentrations at its location of these three "morphogen" chemicals. c) An unspecified molecular mechanism "interprets" the combination of three morphogen concentrations. (For example, if concentration #1 were 22% maximum, and #2 were 55% maximum and #2 were 77% maximum, then the unspecified interpretation could be "differentiate into a chondrocyte". The key idea is that diffusion gradients should be twice as steep in half-sized embryos, ten times as steep in tenth-sized embryos, half as steep in double-sized embryos.   Alan Turing's reaction-diffusion system is an alternative way to generate the same striping pattern. In this case, the concentration of some substance (also called a morphogen) varies along the length of the animal in a regular manner, creating a "pre-pattern" for the eventual stripes in the animal. " ** The chemical morphogens of positional information are very different that what Turing invented that word to mean. *** The spatial variation of morphogen concentrations does not form any geometric >pattern (other than linear, or at least monotonic gradients). **** Most developmental biology textbooks do not distinguish between these uses of the word "morphogen". Sometimes they mean one definition, sometimes they mean the other!   ******************************************************* Things to think about: Nobody has yet proven that any particular spatial pattern of either animals or plants really uses the logical equivalent of this (or other) reaction-diffusion systems. How would you prove (or conclusively DIS-prove) that something like stripes on a Zebra, or on a Zebra Fish, are generated by a reaction-diffusion system? What if you mutated the gene that codes for the "Morphogen" chemical "A" or "B"? What would the phenotype of such a mutation be? Suppose you inserted the amino acid sequence for GFP (green fluorescent protein) into the gene for protein A, or B (even assuming proteins? What would happen if you isolated substance "A" or "B", and put drops of these substances on a developing embryo, where it was forming spots, or somites were splitting apart from each other? How would the spatial pattern be changed that would prove that the isolated chemical really functions like "A" or "B". Suppose that you somehow knew for sure that chemicals A and B were among 10 or 20 chemicals that someone had isolated from body fluids of some kind of embryo; please design an experiment by which you could prove which of the purified chemicals is "A" and which is "B". Next, suppose that an embryo forms regularly-spaced spots. Can we invent a method for extracting substances "A" or "B". By that I mean, to extract them before you know what chemical they are. NOTE: Auxin was purified from oats before it was known for sure to exist. Serotonin was purified from blood when its existence was still hypothetical. Shouldn't hypotheses include experimental criteria for detecting, not just whether they are capable (in principle) of producing a given effect, but also testing where and when and whether that category of mechanism is going on? Not just a litmus test for acidity, but also a litmus test for "morphogen" chemicals, and even a litmus test for whether a reaction-diffusion is or is not the cause of some particular breaking of displacement symmetry.   Please graph concentrations of "A" on the x axis, and graph concentrations of "B" on the y axis, and for a few dozen points in A, B space, please graph little vector-like arrows that illustrate the changes on local concentrations of "A" and "B" as a result of their effects on their own and the other one's concentrations. For example, the arrows in the lower right (corresponding to A being more concentrated than B) therefore point diagonally upward and further to the right. That's because concentrations of both A and B would increase there. Conversely, the arrows in the upper left would point diagonally downward and back further to the left. A diagonal band of very short or zero-length arrows would slope upward and rightward from the point that represents A and B being zero. Such graphical representations of the net effects of combinations of equations are called "phase planes". By using phase planes, your brain can learn to recognize what net effects would be produced by any arbitrary combinations of equations. Phase planes can also be used to do the reverse, which is to invent combinations of equations that will, acting in combination, produce any desired combination of net effects. Incidentally, only those combinations of chemical reactions that produce diagonal boundaries between zones where arrows are pointed in opposite directions parallel to boundary. Can you invent "rules" whose phase plane representation will have a diagonal boundary running from upper left down to lower right, with the arrows above this boundary pointing parallel to this boundary, and in opposite directions on one side of the border as compared with the other side of the border. With effort, you can gradually become able to visualize what a phase plane has to look like in order to be able to break displacement symmetry.