Embryology Biology 441 Spring 2011 Albert Harris
Generation of spatial patterns
-
Imagine that there are two diffusible chemicals "A" and "B"
that obey the following combination of three rules.
2) "B" stimulates breakdown (or removal, or inactivation) of "A" and "B".
3) "B" diffuses faster than "A" (or in any way produces longer range effects).
What results will be produced, from applying these rules over and over?
(Starting from a situation of roughly equal concentrations of both A and B.)
I) Would you have expected any particular results?
II) Can you figure out how the diffusion rates alter the result?
III) How will the results be affected by limiting A to some maximum concentration?
IV) Can you systematically figure out what other combinations
of chemical reactions will produce the same or similar results?
V) By what experimental methods could you answer such questions?
Scott Gilbert's textbook (for some reason) calls "A" and "B"
"Activator" (="P") and "Inhibitor" (="S").
His rules differ from mine in that his S doesn't inhibit itself.
(and it will work that way, & many other variations also will give patterns)
But his color illustration is somebody's plausible guess; not an actual simulation.
They think that such mechanisms only magnify initial irregularities, and make their illustration fit that false guess.
Possible methods to discover such sets of rules that will create spatial patterns
Have an IQ above 200? That might not be high enough!
Find actual chemicals that obey these rules?
Be able to write simple computer programs, such as in BASIC, Pascal, Python, C or Java.
* The results of obeying these three rules would be to generate wave like patterns of concentrations of both A and B. (Turing invented the word "morphogen" to refer to chemicals that create spatial patterns like this.)
** The peaks will become closer together if diffusion rates are more different.
*** Capping maximum concentrations stabilizes the pattern.
"Experimental programming" can answer many biological questions, and there is no better way to predict effects of complex phenomena. Usually, that is the only method that works.
Back in the 1980s & 90s, it was normal for many students in this course to know one or two programming languages, and the university provided them. The "Computer Initiative" ended this, while pretending to do the opposite.
Simple computer programs easily reveal effects of combinations of rules like those listed above, and immediately carry you far beyond what even the smartest person's intuition can achieve.
These wave-like patterns are an example of a reaction-diffusion system.
These were invented by the great British mathematician, Alan Turing,
in the early 1950s, a couple years before he was driven to suicide.
The Apple emblem is believed by many to have originated as a tribute to Turing,
whose method of suicide was to take a single bite out of a poisoned apple.
(I would be very grateful to find out for sure whether this is really true or not.
One alternative is that it refers to the apple in the Book of Genesis.)
Turing designed some of the first computers, proved an equivalent to Godel's Proof, and was the key person who broke the German Enigma Code in World War II. Several biographies and one stage play have been written about Turing's life & death. Prigogine and Meinhardt both claim they independently invented the concept of reaction-diffusion systems, and have published books and research papers on the subject. It is known from Turing's diaries, that Prigogine visited him, and was told about the subject many years before his claimed independent invention. Later, Prigogine got a Nobel prize.
Arthur Winfree did much interesting research on an actual set of chemicals that react together to produce moving waves (that had been discovered in Russia by Belousov and Zhabotinsky). Moving waves are interesting in the case of slime mold chemotaxis, and extremely important for understanding heart contraction waves, which can become chaotically disorganized ("fibrillation"). It is traditional to say that a fibrillating heart has "stopped", and that the electric shock of a defibrillator "restarts it"; but the truth is almost the exact opposite. Defibrillators shock the heart in order to re-synchronize the electric depolarization waves. Even physicians often misunderstand these fundamental concepts.
Scott Gilbert's excellent textbook says that mathematical basis of reaction diffusion systems are "complex polynomial systems" and a "series of partial derivatives depicting rates of synthesis, degradation and diffusion of the activator and inhibitor molecules", which he says are analogous to the harmonics of vibrating strings, in the sense of selectively favoring certain wave-lengths, depending on the equations and the shapes of the area where they operate. Please don't be intimidated by this portentious mumbo-jumbo; Gilbert did the best he could with material he doesn't understand. If you could program, then you could make real discoveries on these subjects.
An aspect of this subject that Scott Gilbert's textbook gets absolutely right is the value of analyzing changes produced by mutations on actual fish color patterns, as compared with changes produced in reaction-diffusion patterns by adjusting some of the reaction rules. If you can match effects of particular changes in equations to effects of particular mutations, then eventually scientists can achieve the kind of progress that connected Mendel's abstract rules to their chromosomal causes.
Surprisingly many different combinations of chemical reaction rules will generate waves of concentration changes - not just the particular equations stated above and in the textbook, both of which are very different from the ones Turing invented, although the principles overlap. For example, some equations produce alternating waves, in which one morphogen chemical has its maximum concentrations at locations where the other morphogen has its minimum concentrations.
The rules about A and B would also produce patterns if A and B increased at locations where A was more concentrated than B, and both decreased at locations where B was more concentrated than A. Furthermore, neither morphogen actually has to diffuse: it is enough that they act at long range, with the inhibitory one acting at longer range. In fact, A and B don't have to be substances: just quantitative variables; Stopak, Greenwell and I got these same patterns to be generated by variations of cell population density and amounts of tension produced by cells in collagen sheets. Logically equivalent ecological situations have been imagined, in which species B is a predator on species A, etc. A German mathematician analyzed many analogous pattern-generation instabilities, including, what might happen inside a nuclear reactor if neutron density and temperature affected each other according to anything like the rules for A and B, stated at the beginning. Would that be a good thing, or a bad thing?
Please don't be put off by the open-endedness of this subject, nor by the mumbo-jumbo: "Complex polynomial systems"? Series of partial derivatives?" Forsooth! Such verbiage is a smoke-screen for people who would rather that you be impressed than that you understand. Scientific and medical progress depends on reaction-diffusion systems eventually becoming as much a part of average common-sense as are negative feedback as a means of creating stability, and positive feedback as a source of self-amplification of small initial changes. These are fields where you could make major contributions, clearing away smoke.

One real reaction-diffusion system is called Liesegang Rings (or Liesegang bands). This occurs if you dissolve dichromate ions in an agar gel, and then let high concentrations of silver ions diffuse into the gel from a point, or from one side. Silver dichromate salt precipitates out in dozens or hundreds of bands, which are separated by clear areas without precipitate. These clear areas are what is surprising.

You can also get spotting patterns that look like the rear ends of Appaloosa horses. This phenomenon was accidentally discovered in efforts to improve photograph film in the 1890s, and has been the subject of many entire books and more than 4,000 published research papers. But nobody has been able to discover the causal mechanism. (Incidentally, dichromate ions [chromium in the +4 oxidation state] are a dangerous poison, and will accumulate in the body. Hundreds of other combinations of ions will also produce Liesegang rings, and you can also use different gels, or very narrow tubes. Dozens of alternative theories (or maybe 100s) have been tested, but then proved not to be the real cause of the Liesegang phenomenon. All such alternatives deserve consideration as possible causes of biological striping and spotting patterns.
An unexplained peculiarity of many striping patterns on animal skins is that the dark lines are darkest right at their edges, and/or the light areas are lightest at their edges. Copperhead snakes are a good example of dark stripes being darkest at their edges, as seen in this recent photograph of a snake caught in our car-port, and then released safely in the forest.

I assume that something fundamental about the pattern-generating mechanism causes this effect, which curiously also occurs in mathematics (and mechanics) when you try to approximate a square wave with sums of sine waves. In that context it is called "The Gibbs Effect", after the Yale professor who invented vector analysis and much of thermodynamics. Until more is known, we can only guess whether there is anything fundamental in common between that effect and the darkening edges of stripes on animal skins. It's either very profound or a coincidence.
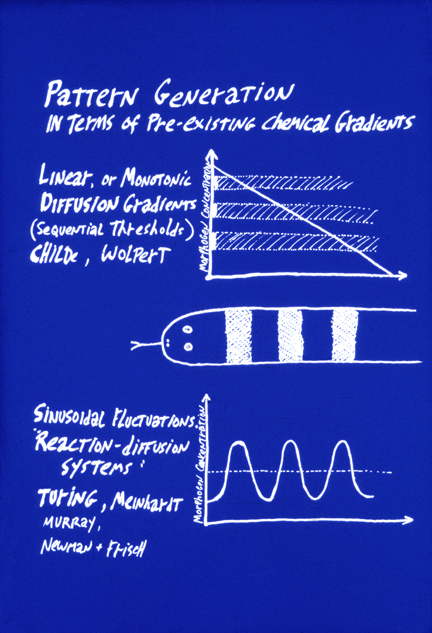
The word "prepattern" is used by embryologists to refer to situations in which the shape of an organ is caused by some chemical or other signal having been distributed in the same geometric locations where the organ is to form. For example, if cells differentiated into cartilage cells wherever a morphogen substance was more concentrated than some threshold amount, and for some reason there was a square area of high concentration of this substance, that is a possible way that an embryo could cause the formation of a square cartilage. Thus, reaction-diffusion systems were invented as a way to create pre-patterns. Apparently, it didn't occur to Turing that mechanical analogs to his sets of rules could directly create geometric patterns; but this has always been a blind-spot to 99% of embryologists, whose logic seems to be that since genes are chemical in nature, therefore anatomical patterns should be generated first as patterns of chemical concentrations of some kind of signaling molecules, that cells then respond to by differentiating into whichever cell type is appropriate for each location. That paradigm has been so dominant, for so long, that people forget it's a working assumption, not a logical necessity. But it does seem to be basically correct in many cases.
It is very important to notice the fundamental difference between the concept of prepatterns, as contrasted to the concept of "positional information". The latter also depends on diffusion concentration gradients of chemical signal molecules, but in the case of positional information, these concentrations supposedly tell the undifferentiated cells where they are, relative to the rest of the body, in contrast to telling cells what to differentiate into. To return to the imagined example of the square cartilage, positional information would cause its shape by stimulating differentiation at whatever locations in the embryo had concentrations of two different morphogens that were above one threshold but below another threshold. The morphogen concentrations would not have the shape of any of the organs they caused to form. The shapes would arise at the "read-out" stage of the process, at which many different concentrations of morphogen concentrations would be "interpreted" by cells as meaning that they should differentiate as cartilage. The idea is that positional information tells each cell its latitude, longitude and altitude, by means of two or three approximately perpendicular, and at least monotonic if not necessarily linear, concentration gradients. Instead of causing a given organ to differentiate where some pre-pattern chemical's concentration is above (say) ten units, the central idea of positional information is that an organ will form where cells detect that the concentration of morphogen X is between 65% of maximum and 70% of maximum, AND the concentration of Y is between 23% of its maximum and 34% of its maximum.
If this does not seem to you to be a fundamental difference, between pre-pattern hypotheses as contrasted with positional information hypotheses, then please keep thinking until you see that they are radically different. Both use diffusion gradients, which in both cases control what cell type embryonic cells will differentiate into. Furthermore, reaction diffusion mechanisms can be used to create monotonic gradients (for positional information), by setting the variables to make the wave length longer than the length of the embryo. But the concept of positional information is fundamentally and completely different than pre-patterns: not that I particularly support either one. Some of those teaching the Cell & Development course don't understand that there is a difference, I think because they are so much more interested in finding out the chemical nature of the signal molecules. "Earth goes around the sun; Sun goes around the earth?" is that just a semantic difference? And what matters is what they are made of?
The motivation for the theory of "positional information" is to be able to account for the phenomenon Driesch discovered ("Embryonic Regulation"). How can adjustment of the sizes of parts of an embryo be explained by pre-patterns? To phrase this question another way, how could pre-patterns for organs each become proportionally smaller in response to separating the first two cells of an echinoderm embryo? Or why would pre-patterns become twice as big in response to fusing two embryos together? The observed facts are that component parts do adjust sizes in proportion to the size of the whole, over as much as an 8-fold range of volumes in echinoderms, and over more than a hundred-fold range of volumes in Dictyostelium. Therefore, we have to worry about how the causal signaling mechanisms accomplish this adjustment of sizes of parts in proportion to changes in sizes of the whole.
This fundamental problem was emphasized by the British embryologist Lewis Wolpert, who coined the term "positional information", and developed a deceptively useful analogous to the French flag. He also wrote an embryology textbook that we tried for two years in this course, has written diverse books on subjects from depression to understanding impossibilities, and is one of the most stimulating conversationalists I ever met, although I mostly disagree with him. Wolpert asks us to imagine a flatworm with only three differentiated cell types, arranged in the pattern of the French flag: One-third red cells, one-third white cells, and the other third blue cells. Also imagine that their differentiation was controlled by local concentrations of a single diffusing "morphogen" signal chemical (notice that he appropriates the word that Turing invented, and uses it to mean something fundamentally different. (If you ever want to muddle a difficult issue, there is much to be learned here.) The first key idea is that a linear gradient could stimulate cells to differentiate into the red cell type wherever the morphogen concentration exceeds two-thirds of maximum, and intermediate concentrations of this same morphogen chemical would stimulate cells to differentiate as white cells, and concentrations lower than 1/3 maximum would cause differentiation of blue cells.
Then the second key idea is that cutting such an animal into halves would cause the concentration gradient to become twice as steep. (We are asked to suppose.)
Therefore, the red, white and blue bands would all adjust in proportion to the new dimensions of the worm fragments. Hundreds of biologists fell in love with this pair of ideas; and thousands more followed them, believing that the idea was that something has to tell each cell type where to differentiate. Notice our textbook's enthusiasm for the idea of a graft from an American flag, resulting in formation of a little bit of red stripes down in one corner. An actual experiment equivalent to this was Oscar Shotte's grafting of mouth tissue from salamander embryos to frog embryos, and vice versa. His result was that suckers developed from frog tissue, and jaws formed from the salamander tissue. That meant that frog and salamander embryos respond to each other's signals, which is an entirely different issue from whether these signals act as prepatterns as opposed to positional information. Smart people are never bigger suckers than when they hope they are having a profound insight.
The discoveries of bicoid protein gradients in early fly embryos by Wieschaus and Nusslein-Volhard earned them a Nobel Prize, and may yet win that prize for Wolpert himself. It cannot be denied that these and some other embryonic gradients are very close to what Wolpert had guessed. Ironically, fly development is very mosaic; whereas the gradients were postulated as explanations for regulative development. Furthermore, early development in arthropods differs radically from most other animals, in that the embryo remains syncytial until about the 6,000 cell stage. Only that allows molecules as big as transcription factors to diffuse the length of the embryo.
Nevertheless, those of us who have argued against Wolpert feel like the cartoon Coyote, watching the Roadrunner zoom through the tunnel painted on the side of a cliff.
Creative imagination is always a good thing, but so is critical reasoning.
The point of the following drawings is that for flags even slightly more complex than France's and Russia's, cell differentiation would need to be controlled by ratios of morphogen concentrations. It's not impossible, but detracts from the attractive simplicity promised by positional information. I have written Pascal programs that use two perpendicular gradients to produce U.S., Czech, Japanese, British and Confederate flags, and allow the user to add arbitrary sinks and sources of both morphogens.
I wish we had a Java version of this program, so that we could put it on the web site, for you to try.

