Embryology Biology 441 Spring 2012 Albert Harris
Symmetry
A brief but necessary digression about the concept of symmetry, and "symmetry breaking".
What key ideas about symmetry do you need?#1) There are more kinds of symmetry than reflection symmetry.
Displacement symmetry (somites, for example; and ions in crystals; Many examples in two and three dimensions; stripes & dots on animals.
Dilation symmetry (magnification or shrinkage)
Remember Driesch? Remember slime-mold slugs & fruiting bodies?
Rotation symmetry (propellers, snail shells)
Combinations can occur between two or more kinds of symmetry:
...between rotational and dilation symmetry in snail shells: Magnify by 50 % equivalent to rotation by some number of degrees
...between reflection and displacement in "glide reflection" symmetry.
Given a letter of the alphabet, or a drawn shape, can you state which kinds of symmetry it has, or which combinations? A, B etc N, S etc. H, I, 8 etc. * etc.
#2) Weyl's way of defining symmetries:
"...If there is something you can do to it, and it looks the same.. (reflect it, displace it, rotate it...distort it...anything that leaves it looking the same, then the thing has reflection symmetry, displacement symmetry, rotational symmetry)
Notice this allows you to invent/discover your own new kinds of symmetry, that are useful for comprehending how embryos create shapes.
Most (all?) embryological shape changes are reductions in some symmetry.
Somite formation reduces from infinite displacement symmetry to displacement symmetry by just certain amounts. Likewise, consider a spherical embryo loosing infinity minus one planes of reflection symmetry.
(Is it helpful to consider conjoined twins as having lost infinity minus two planes of reflection symmetry?)
#3) Not just objects have particular symmetries, so do forces and processes.
In the clock & wave-front theories of somite formation, a time-displacement symmetry produces a reduced space-displacement symmetry (somites)
If the forces causing a shape have spherical symmetry (the same strength in all directions), then what shape will these forces create?
In order to make a less symmetrical shape, what property has to change?
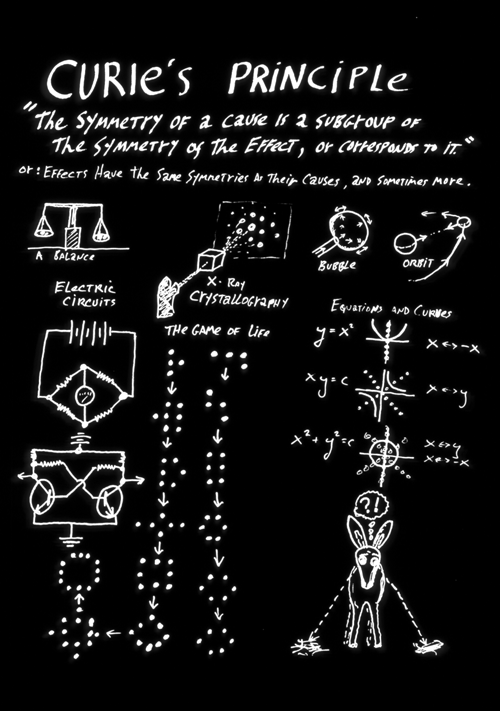
#4) Curie's Law, and embryological mechanisms that evade this law.
Effects can't have less symmetry than their causes. (no problem gaining symmetry)
For example, can spherically symmetrical forces produce square shapes? What shapes can they produce.
If a crystal structure has inversion symmetry with respect to electrical charges, can it be piezoelectric? No, it can't. And the converse is also true! Piezoelectric properties are caused by NOT having inversion symmetry of charge.
This is how Curie, a co-discoverer of piezoelectric effects, got interested in how to relate phenomena to symmetries, maybe a bigger discovery than co-discovering radium!
Oh, yeah? Let's see somebody destroy a city with symmetry? ...besides Le Corbusier!
#5) How to evade Curie's Law (become less symmetrical, but not randomly) is THE central problem of developmental biology.
This opinion is shared by nearly all biologists who collect books on symmetry, which is hardly any.

What methods do embryos use to make themselves less symmetrical, but without becoming random?
This is a central question of Embryology;
arguably THE central question,
when you learn all the different kinds of symmetry,
but very few embryologists understand enough math & physics to know it.
How to develop the same asymmetries every time, such as the right/left asymmetry?
___________________________________________________________
Why are oocytes and early embryos spherical?
(in most kinds of animals, although NOT flies)
It's because their shapes are caused by counterbalances of highly symmetrical forces.
The outward fluid pressure inside an oocyte, has equal strength in all directions (= is spherically symmetrical).
The contractile and elastic tension in its surface also have equal strength in all directions (parallel to this surface)
Symmetrical forces create shapes with the same symmetries as the forces
Most people are not used to thinking of forces as having symmetries,
but they do. Even algebraic equations and laws of nature have symmetries.
The conservation of energy, momentum, electric charge, angular momentum etc.
each result from particular symmetries in laws of physics. (don't worry about this)
For us, the important fact is that to create a less symmetrical shape, some of the forces would have to be stronger in some particular direction.
(in other words, some force would have to be less symmetrical
then the shape of the embryo can also become less symmetrical, and have the same reduced symmetry as the force that causes this change.)
When anything becomes less symmetrical, that is called "symmetry breaking", although it doesn't necessarily mean anything is breaking, just that something is becoming less symmetrical than it had been until then.
________________________________________________________________
Example:
Visualize an ordinary dinner plate and a drinking glass;
they both have axial symmetry.
Their geometry is symmetrical about a vertical axis:
the same in all sideways directions from a vertical axis through their center.
They don't have the same shape; but they do have the same symmetry.
If you drop a glass or a plate on a hard surface, it probably will break into many asymmetrical pieces.
That is a crude example of symmetry breaking, and not difficult.
Much more difficult would be to break a glass or a plate so that it broke into two symmetrical halves;
and even more difficult would be to break them consistently into slightly different right and left halves.
Embryos manage to break symmetry with consistent results. ___________________________________________________________________________________
First concept: How to define symmetry?
Consider the capital letter A.
If we reflect an A in a mirror, it looks (almost the same).
It has a vertical plane of "Reflection Symmetry"
The letters B, C, D and E all have horizontal planes of reflection symmetry.
? What other letters have planes of reflection symmetry (I count a total of 17)?
(but you might not agree with me about L having a diagonal plane of reflection symmetry)
What about the letter H?
H has a vertical plane of reflection symmetry,
and also has a horizontal plane of reflection symmetry.
(two, non-equivalent planes of reflection symmetry
The letter "I" also has two perpendicular planes of reflection symmetry.
What symmetries do the numbers 8 and 0 have?
What about the symbols * , + , - , ^ ,<, > and %?
A circle has an infinite number of planes of reflection symmetry,
all of which are equivalent to each other.
(Notice the contrast with H, 8 and 0, and squares,
all of which have non-equivalent planes of symmetry.
A square has four planes of reflection symmetry, 2 of one kind & 2 of another)
Most embryos start out with an infinite number of planes of symmetry, like a cone, or a hemisphere, dinner plate or water glass. ("axial symmetry") And then special mechanisms reduce = "break" symmetry.
Mammal oocytes come close to having spherical symmetry, but for most kinds of animals, the yolk is more concentrated near the vegetal pole from the very beginning, so they never have more than axial symmetry.
Formation of the grey crescent breaks axial symmetry and replaces it with one plane of reflection symmetry.
This amounts to the destruction of infinity-minus-one planes of reflection symmetry.
Second big concept: There are more kinds of symmetry than just reflection.
Please consider the symmetry of the letters S, N and Z.
They all have two-fold rotational symmetry.
A three-bladed propeller has 3-fold rotational symmetry.
A swastika has 4-fold rotational symmetry, etc.
The internal microtubule structures of cilia and flagella have 9-fold rotational symmetry, but do not have reflection symmetry.
Vertebrate embryos use this lack of reflection symmetry to control creation of Right-Left differences, (very much like the "Right Hand Rule" in the physics of electromagnetism.)
Mutants (including mutant humans) who lack beating flagella nevertheless develop right-left asymmetry
more kinds of symmetry
Consider the symmetry of the following pattern @@@@@@@@@@@
This has displacement symmetry.
A line _______________________________________
can be said to have infinite displacement symmetry, in that it it looks the same for any (small or big) amount of displacement. but this line -------------------- only has displacement symmetry for displacements of a certain distance. (a sine wave is another example). When an embryo becomes segmented, & when it forms somites, Then it is "breaking" displacement symmetry.
QUESTION FOR CLASS DISCUSSION:
Turing's reaction-diffusion mechanism serves to break what kind of symmetry?
Even more kinds of symmetry
Another kind of symmetry is dilation symmetry.
(When something continues to look the same when magnified)
Snail shells have combined rotation and dilation symmetry;
Certain amounts of rotation produce the same apparent change
As certain amounts of magnification.

Certain phenomena look the same at different size scales.
Mathematicians and engineers say that these phenomena "scale"
I recently bought an applied physics book titled "Scaling", which is about variations in the extent to which physical phenomena (explosions, for example) produce the same shapes ("mushroom-shaped clouds" for example) over wide ranges in sizes.
Self-Symmetry of Fractals is also amusing. (but please don't let yourself get carried away with fractals & chaos theory; neither is a hundredth as important as the principles of symmetry).
You can invent new kinds of symmetry, such as reflection in a distorting mirror
A Third big concept, related to symmetry
Stability different kinds of stability
Divergence away from a stable state: Can break symmetry.
Is achieved either by positive feed-back, or loss of negative feedback
Convergence toward a stable state (can create shape, & create symmetry)
Is best achieved by negative feed-back, homeostasis

You will not be tested on this physics, about conservation laws.
But I hope it will be as stimulating to you as it is to me:
Like a view from the top of a very high mountain.
For every symmetry, there is a conservation law.
Displacement in time → behave the same→ Conservation of Energy
Displacement in space → behave the same→ Conservation of Momentum
Rotation of angle → behave the same → Conservation of Angular Momentum
Change in quantum mechanical phase → → Conservation of Electrical Charge
These facts were discovered by Prof Emmy Noether, of Bryn Mawr College, one of the 3 Quaker colleges in the suburbs of Philadelphia.
To quote Richard Feynman:
This is... probably the most beautiful and profound things in physics,
but I am sorry that I can’t explain it in any way how it comes about.
What about symmetry with respect to mirror image reflection?
No! Experiments have proven that "Parity is NOT conserved" (unless, you also interchange matter and antimatter)
Now we return to facts that you WILL be tested on, on future exams.
Spherical symmetry (for example, of a soap bubble)
Axial symmetry (of a cone, unfertilized urchin or human oocyte, or an early urchin gastrula, or an early mammal blastocyst)
One plane of mirror reflection symmetry (a pluteus, the exterior of the human body, The letters A, B, C, D, E, K, M, T, U, V, number 3)
Two planes of mirror reflection symmetry (The letters H, I, number 8, 0)
Three or more planes of mirror reflection symmetry (A starfish, a sea urchin, a jelly fish, an individual coral animal, octopus, some other invertebrates, and plants;
diatoms are especially interesting examples, the symbol *, the letter Y, almost).
Axonemes of cilia and (eukaryotic) flagella have 9-fold rotational symmetry.
Two-fold rotation symmetry: (The letters N, S, Z, $, %, #, two-bladed propellers for airplanes and boats)
Three-fold rotation symmetry: Three-bladed propellers.
Glide-reflection symmetry: WWWWW , approximately.
There are many good examples in crystal structures and animal color patterns.
Displacement symmetry: somites, ties along a railway, spots on an animal Legs on a centipede or millipede.
"Displacement-distortion symmetry": ribs, vertebrae, legs on a crayfish.
"Dilation symmetry" Driesch’s discovery about embryonic regulation.
Branching patterns of gland and kidney ducts; fern leaf patterns.
"Dilation-displacement symmetry" A long cone, or other shape that tapers in size.
"Dilation-rotation symmetry" A snail shell
Remember Weyl’s definition: A thing is symmetrical, if there is something you can do to it, after which it looks the same as it did before.
So if you have a pillow-case, or a sleeping bag (or some organ in the body, or some kind of invertebrate, that looks the same after you have turned it inside out, therefore it has turned-inside-out symmetry! (Which I just this minute invented!)
Please try to invent some new kinds of symmetry.
Biologists have been left far behind:
For example biologists usually consider only two forms of symmetry - "mirror image symmetry" (Plutei) and "radial symmetry", starfish.
Radial symmetry is naively said to be evidence of evolution from sessile ancestors.
Reduction of anatomical symmetry from axial to mirror image symmetry is said by biologist to be the development of symmetry.
Really, it’s the destruction of infinity minus one planes of reflection symmetry!
(NOT the formation of a new plane of reflection symmetry.)
Imagine somebody who had a million dollars, and lost all but one of them;
then describing what had happened as finding one dollar.
Despite backgrounds in physics and mathematics, Turing, Meinhardt and the advocates of "Clock and Wave-front" theories do not think of these mechanisms as breaking displacement symmetry.
Liesegang rings also break displacement symmetry, and produce a displacement-dilation symmetry (rings progressive farther apart and wider. Also slower to form?
Air pressure inside a soap bubble has spherical symmetry.
Surface tension has axial symmetry, at each location.
Soap bubbles are therefore spherical.
In order to blow square bubbles, either the pressure or the tension will need to have less symmetry (the symmetries of a cube)
The directional elongation of growing cartilages cannot be caused by stronger osmotic swelling in the long axis, because osmotic pressure is a scalar (and has spherical symmetry).
The elongation must be caused by directionality of "Young’s Modulus" or possibly by directionality of tension.
Sperm entry location breaks radial symmetry of amphibian eggs
(stimulates formation of the anterior-posterior axis).
And when fertilization happens to occur exactly at the animal pole,
then gravity stimulates formation of the anterior-posterior axis.
In nematode embryos, Prof. Bob Goldstein proved that the location of sperm entry Also breaks symmetry, and stimulates formation of the anterior-posterior axis.
In bird eggs, the direction of the anterior-posterior axis is believed to be initiated by the direction of gravity.
In mammal eggs, it hasn’t yet been discovered what "breaks" either spherical or axial symmetry.
But breaking of right-left symmetry in humans is caused by flagella in the primitive node. This was discovered because of Karteganer’s syndrome, which is caused by a mutation that paralyses flagella and cilia.
About 45% of people born with this syndrome have a reversed asymmetry of their aorta and stomach; another 45% have normal asymmetry of anatomy, and around 10% have partial reversal of right left asymmetry of internal organs.