Lecture notes for Friday, February 13, 2015
Key points about cell locomotion and pattern formation
#1) >Cells crawl using > 6 or a dozen fundamentally different mechanisms
(most of which get their force from cytoplasmic actin).
#2) Amoeba proteus locomotion is very different even from white blood cells.
They both use actin polymerization, but in different ways:
-
* To cause gel tube formation in Amoeba,
** To slide along the inside of the plasma membrane in cells of our body.
video of a fibroblast on a rubber substratum
#4) This crawling locomotion creates many anatomical structures. (Remember the video of the blood vessels extending and branching, shown on February 9th ? Paths and sizes of veins and arteries are created by where cells crawl, instead of where they differentiate.
Another example is that all skeletal muscle cells begin along the back, and move from there to arms, legs, tongue, etc. Where they differentiate has nothing to do with their eventual locations or connections.
A third example is that all pigment cells begin along a different part of the back.
Therefore skin color patterns are created by where cells crawl, where they
complete differentiation, and where they don't self-destruct.
In sponges, all differentiated cells constantly rearrange all the time. Not just sorting out when dissociated, as H. V. Wilson discovered. Where sponge cells differentiate has nothing to do with eventual position.
video of sponge cells rearranging
Regarding the hope for using stem cells to replace anatomical structures, it won't be enough just to control where cells differentiate; Controlling active rearrangement will also be needed.
So strong that it rearranges and aligns collagen into what look like tendons.
David Stopak and I proposed a hypothesis that collagen rearrangement, instead of just cell locomotion is really the main embryonic function of mesenchymal traction.
Another idea is that trauma stimulates mesenchymal cells to switch to being "myofibroblasts", whose function is to construct wounds (and repair tendons, but not to build tendons in the first place.
Please invent experiments that could prove or disprove our tendon formation idea.
Regarding Turing's mechanism of pattern formation.
#6) Simple combinations of rules can create geometric patterns.
A simple example of a general principle:
-
i) "A" stimulates synthesis (or release) of both "A" and "B".
ii) "B" stimulates breakdown (or removal, or inactivation) of "A" and "B".
iii) "B" diffuses faster than "A" (or in any way produces longer range effects).
Scott Gilbert's widely-used textbook calls "A" "the Activator" (="P")
and calls "B" the "Inhibitor" (="S").
His rules differ slightly from mine, in that his S doesn't inhibit itself.
Turing's original rules were even more different in (uneccessary) details.
Many other variations also will patterns of stripes and spots.
#7) Many people assume that animal color patterns must be caused by reaction-diffusion systems. This is the good old "What else could it be?" argument.
But it still hasn't been proven in even a single case. Computers prove that it could work.
Some arguments AGAINST Reaction-Diffusion as an embryological mechanism.
- The spots and stripes are not as regular as real animal patterns.
(The spots calculated in Turing's original computer programs were blobs)
[But that problem can easily be fixed]
- Sizes and spacing between stripes do not regulate (such as Driesch observed).
Diffusion rates and/or reaction rates might change in smaller animals, so that stripes etc. would change size in separated cells.
Anyway, some animal color patterns don't regulate.
Tensor variables can produce the same, or more complicated, geometric patterns.
Anatomical structures can be directly created by physical variables.
Cartilages and feather papillae were the examples that we proposed.

If you get interested, look at the many papers by George Oster and Jim Murray.
#9) Liesegang Rings
Chemists accidentally discovered that many combinations of ions create stripes and spotted patterns. Dissolve dichromate ions in an agar gel, and then let high concentrations of silver ions diffuse into the gel from a point, or from one side. Silver dichromate salt precipitates out in dozens or hundreds of bands, which are separated by clear areas without precipitate. These clear areas are what is surprising.

This phenomenon was accidentally discovered in efforts to improve photograph film in the 1890s, and has been the subject of many entire books and more than 4,000 published research papers. Dozens of alternative theories (or maybe 100s) have been tested, but then proved not to be the real cause of the Liesegang phenomenon. All such alternatives deserve consideration as possible causes of biological striping and spotting patterns.
An unexplained peculiarity of many striping patterns on animal skins is that the dark lines are darkest right at their edges, and/or the light areas are lightest at their edges. Copperhead snakes are a good example of dark stripes being darkest at their edges, as seen in this photograph of a snake caught in our carport, and then released safely in the forest.

I assume that something fundamental about the pattern-generating mechanism causes this effect, which curiously also occurs in mathematics (and mechanics) when you try to approximate a square wave with sums of sine waves. In that context it is called "The Gibbs Effect".
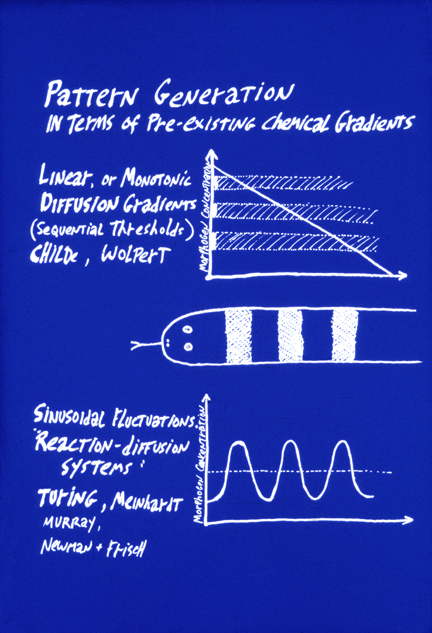
#10) The word "prepattern" is used by embryologists to refer to situations in which the shape of an organ is caused by some chemical or other signal having been distributed in the same geometric locations where the organ is to form. For example, if cells differentiated into cartilage cells wherever a morphogen substance was more concentrated than some threshold amount, and for some reason there was a square area of high concentration of this substance, that is a possible way that an embryo could cause the formation of a square cartilage. Thus, reaction-diffusion systems were invented as a way to create pre-patterns. Apparently, it didn't occur to Turing that mechanical analogs to his sets of rules could directly create geometric patterns.
It is very important to notice the fundamental difference between the concept of prepatterns, as contrasted to the concept of "positional information". The latter also depends on diffusion concentration gradients of chemical signal molecules, but in the case of positional information, these concentrations supposedly tell the undifferentiated cells where they are, relative to the rest of the body, in contrast to telling cells what to differentiate into. To return to the imagined example of the square cartilage, positional information would cause its shape by stimulating differentiation at whatever locations in the embryo had concentrations of two different morphogens that were above one threshold but below another threshold. The morphogen concentrations would not have the shape of any of the organs they caused to form. The shapes would arise at the "read-out" stage of the process, at which many different concentrations of morphogen concentrations would be "interpreted" by cells as meaning that they should differentiate as cartilage. The idea is that positional information tells each cell its latitude, longitude and altitude, by means of two or three approximately perpendicular, and at least monotonic if not necessarily linear, concentration gradients. Instead of causing a given organ to differentiate where some pre-pattern chemical's concentration is above (say) ten units, the central idea of positional information is that an organ will form where cells detect that the concentration of morphogen X is between 65% of maximum and 70% of maximum, AND the concentration of Y is between 23% of its maximum and 34% of its maximum.
The motivation for the theory of "positional information" is to be able to account for the phenomenon Driesch discovered ("Embryonic Regulation"). How can adjustment of the sizes of parts of an embryo be explained by pre-patterns? To phrase this question another way, how could pre-patterns for organs each become proportionally smaller in response to separating the first two cells of an echinoderm embryo?
This fundamental problem was emphasized by the British embryologist Lewis Wolpert, who coined the term "positional information", and developed an analogy to the French flag. He asks us to imagine a flatworm with only three differentiated cell types, arranged in the pattern of the French flag: One-third red cells, one-third white cells, and the other third blue cells. Also imagine that their differentiation was controlled by local concentrations of a single diffusing "morphogen" signal chemical (notice that he appropriates the word that Turing invented), and uses it to mean something very different). The first idea is that a linear gradient could stimulate cells to differentiate into the red cell type wherever the morphogen concentration exceeds two-thirds of maximum, and intermediate concentrations of this same morphogen chemical would stimulate cells to differentiate as white cells, and concentrations lower than 1/3 maximum would cause differentiation of blue cells.
Then the second key idea is that cutting such an animal into halves would cause the concentration gradient to become twice as steep. (We are asked to suppose.) Therefore, the red, white and blue bands would all adjust in proportion to the new dimensions of the worm fragments. Hundreds of biologists fell in love with this pair of ideas; and thousands more followed them, believing that the idea was that something has to tell each cell type where to differentiate.
For flags even slightly more complex than France's and Russia's, cell differentiation would need to be controlled by ratios of morphogen concentrations. I have written Pascal programs that use two perpendicular gradients to produce U.S., Czech, Japanese, British and Confederate flags, and allow the user to add arbitrary sinks and sources of both morphogens.



The discoveries of bicoid protein gradients in early fly embryos by Wieschaus and Nusslein-Volhard earned them a Nobel Prize, and may yet win that prize for Wolpert himself. It cannot be denied that these and some other embryonic gradients are very close to what Wolpert had guessed. Ironically, fly development is very mosaic; whereas the gradients were postulated as explanations for regulative development. Furthermore, early development in arthropods differs radically from most other animals, in that the embryo remains syncytial until about the 6,000 cell stage. Only that allows molecules as big as transcription factors to diffuse the length of the embryo.