Embryology Biology 441 February 8, 2016 Albert Harris
How mechanical forces cause geometrical shapes
Genes -----> Forces -----> Anatomy
11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111
Each has a interior pushing out, inflating a flexible surface.
Ten examples:
a) Hollow blastulas (sea urchins) and blastocysts (mammals)
b) The brain, and the rest of the central nervous system, are a hollow, fluid filled tube.
The pressure of this cerebro-spinal fluid inflates the brain more than the spinal cord.
Lobes of the brain are created by more inflation at certain places than elsewhere.
A simple experiment is to poke a small hole in any part of the neural tube, and reduce the pressure to near zero. Insertion of a hollow glass tube will prevent the hole from closing. This results in the brain lobes not inflating.
c) The eyeball is inflated with a weak gel, which acts like a liquid. Inserting a hollow glass tube through the eyeball will prevent its inflation. (Dr. Coulumbre proved this, at the NIH)
d) Teleost oocytes form their upward-bulging blastodisk by cytoplasmic pressure pushing against a circle where the contractility of the cell cortex is weaker than elsewhere.
e) Cleavage (cytokinesis) of all animal cells is caused by strengthening of cytoplasmic acto-myosin in the circumferential direction in a belt-like contractile ring that pinches the cell in two after mitosis (And separate from the mechanism of chromosome movement in mitosis).
f) Polar body formation is a special unequal form of cytokinesis, that follows each meiotic division of oocytes.
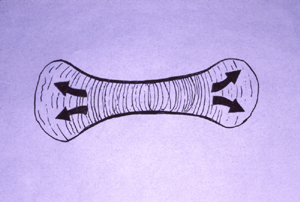
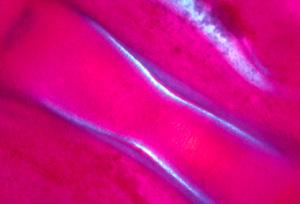
g) Cartilages expand by electro-osmotic pressure pushing outward against resistance of collagen and elastin fibers. These fibers wrap around the outside of each cartilage, and also run through the interior of the cartilage. Visualize water balloons with very gooey water inside, and with nylon threads and rubber bands wrapped around the outside, and also running through the interior.
h) Notochords are tightly packed with weak, vacuolated, jelly-like, cells; and are tightly wrapped with sheets of collagen fibers, running in spirals.
i) Blood vessels (arteries, veins, capillaries) are lined with a special kind of thin epithelial cells named "endothelial cells", which are wrapped by collagen fibers, smooth muscle cells, and fibroblasts. It's an unasked mystery what mechanism wraps them with collagen. Another is why smooth muscle cells orient circumferentially; perpendicular to what contact guidance usually produces!
j) The chambers of the heart?
2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222
Curvature = angular change of the tangent line per distance
(angular change per distance along a curve)
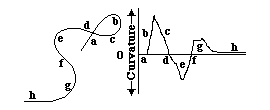


The Radius of Curvature = 1 / divided by curvature
(and has units of distance per radian of angular change)
(also, it is the radius of the circle that would most closely approximate a given section of a curve)
A straight line has zero curvature.
(and its radius of curvature is infinite, please notice)
A circle has constant curvature.
Curvature of small circles is larger than curvature of big circles.
A sphere has constant curvature in all directions .
A plane has zero curvature in all directions.
A cylinder has zero curvature in the lengthwise direction; and has constant curvature in the circumferential direction
.

Curvature of surfaces varies with direction,
for all shapes except for spheres or planes
(on which curvature is the same in all directions)
Differential Geometry is a division of higher mathematics in which shapes are defined in terms of curvatures, instead of the x, y, z coordinates that we learn about in elementary mathematics.
Everybody but mathematicians is much more familiar with Analytic Geometry, which defines shapes in terms of x, y and z coordinates. That is why Lewis Wolpert's "Theory of Positional information" is so plausible and widely believed. He claims anatomical shapes have to be caused by perpendicular diffusion gradients, that act like the x, y and z coordinates.
Such gradients have actually been discovered, especially in early fly embryos.
Examples include the Bicoid protein, "Sonic Hedgehog", and retinoic acid.
But counter-balances of pressures and tensions are just as important: development is a mixture.
Nevertheless, Positional Information is somewhat analogous to "The Ether" in Physics before 1905.
33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333
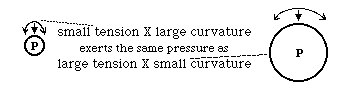
Pressure difference equals Curvature multiplied times Tension.
dP = C x T
dP = T/R where R is the radius of curvature
Because both curvature and tension often vary with direction
dP = C x T + c x t c and t are curvature and tension in the axis perpendicular to C and T
dP = T/R + t/r R and r are radii of curvature in two perpendicular directions
Unfortunately, D'Arcy Thompson and many others mistakenly used this equation
dP = T x (1/R + 1/r) Which assumes that tension is the same in all directions.
For soap bubbles, tension really is the same in all directions.
But for cell sheets and surfaces of living, actively contractile cells, tension usually varies as some function of direction, therefore the correct equations are dP = C x T + c x t = T/R + t/r
This and other simple mistakes have led biophysics down a blind alley.
Complete copy of D'Arcy Thompson's book, On Growth and Form
The same book as a text file (no illustrations but easier to search for key words or topics)
4444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444
How to think about quantitative variables that vary with direction?
(like curvature, tension, permeability, strain, and others).
Variables that don't have any directionality are called scalars.
Chemical concentrations, density, temperature, osmotic pressure, & hydrostatic pressure are scalars.Scalars have an amount at each location , which can differ with location; but has no direction.
Vectors have an amount and a direction at each location.
Electric fields are an example of a vector variable.
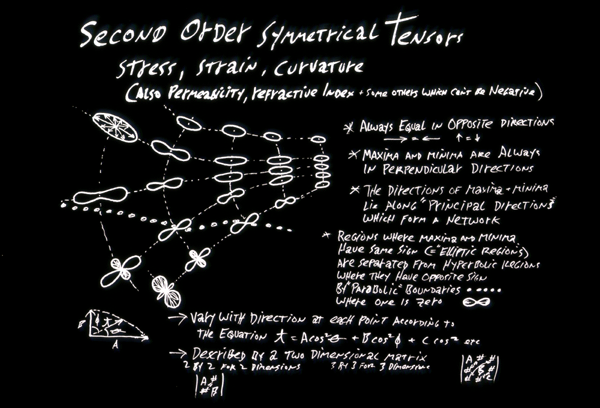
Curvature, tension (equals "stress", which includes tensile stress and compressive stress) and "strain" and permeability are all examples of variables that can and often do have different amounts in different directions.
Variables that differ with direction are called tensors, and unfortunately are not included in the education of anybody but mathematicians and some engineers. In my opinion, tensors are more important for embryology than vectors.
All you need to know about tensors are the following:
1) Curvature, stress (tension) and strain (% distortion produced by stress) are second order symmetrical tensors.
2) (most) Vectors are considered to be first order tensors. Scalars are zeroeth order tensors.
3) Elastic moduli are fourth order symmetrical tensors. That means their variation with direction can be more complicated than if they were second or third order tensors.
4) The word "Symmetric" applied to tensors means that for every two opposite directions, their value is the same.
[Don't worry about it, but axial vectors are really second order anti-symmetric tensors.]
5) For second order tensors, if they vary with direction (which they CAN, but don't have to), their minimum and maximum directions are always exactly perpendicular to each other.
D'Arcy Thompson's biggest mistake was to treat mechanical tension as if it could not vary with direction, which greatly narrowed and reduced how many geometric shapes he could "explain". He could only recognize the possibility of direct causation by forces when objects had shapes that could be produced by tensions that were equal in all directions and at all locations. (spheres, catenoids, etc. the sums of whose curvatures are constant everywhere, as in soap bubbles).
It is a tragedy that so many people have such strong positive or negative responses to D'Arcy Thompson, but nobody analyzes his tacit assumptions, nor why these assumptions are misguided.
Incidentally, tensors played a major role in the escape of physics from the "ether" concept, which was analogous to "positional information" in today's embryology.
D'Arcy Thompson mistakenly persuaded himself and his readers that self-building shapes can only result from tensions that don't vary with direction. Malcolm Steinberg (and Scott Gilbert) became persuaded that convergence to any consistent geometry, via two or more alternative sequences of intermediate geometries, can only be caused by forces that are reversible, conservative and minimize free energy. Mathematicians tend to think that they somehow "own" the concept of tensors, think of them more in the sense of "transformation of number matrices", not as physical variables.
5555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555

Stress = mechanical force per cross-sectional area: Either tensile stress or compressive stress. It has units of force per unit area.
Strain = proportional stretching or compression (produced by stresses)
What % has a material lengthened or shortened. (or sheared)?
If all stresses were relieved, then how much would dimensions change?
Young's modulus = the slope of the curve of stress per strain
Rubber has a small Young's modulus; steel has a large one<.p>
Hooke's law = linear proportionality of stress to strain
If Young's modulus is constant, then a material is "Hookean"
But real materials are never Hookean beyond 1 or 2% strain.
Please understand that Hooke's law is NOT a law of nature.
It is a rule of thumb that is sometimes true.
At small strains (<1 or 2 %) it is true of many materials.
At large strains (>10% it is always more and more untrue)

Also, when Hooke's Law is not obeyed, then
Young's modulus is not constant, & so doesn't really exist.
It's a proportionality constant for a ratio that isn't constant;
or the slope of a curved line (sometimes one with hysteresis!)
(hysteresis in the sense that the pull is stronger for a given % strain when you are applying force, but weaker as you release this stress)

Do not be frightened by tensors. They are your friends.
66666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666
You let me control the Ts and Ps: I can make the Cs do what I want! Even just controlling Ts, and letting P be some constant pressure, then the curvatures are almost completely at the mercy of the Ts.
Developmental biology is about how genes create & control anatomy.
Much is about how curvatures are created by tensions (acto-myosin)
This is very important for plastic surgery, & many other specialties.
To understand these issues (even a little) puts you way ahead of other future MDs.
Visualize a flexible sheet of cells, with fluids on each side, and a pressure difference.
A) What shape will this sheet become if its tension is the same at every location, and in every direction?
Hint: a sphere or a section of a sphere.
B) What shape will it change to if we make the tension stronger in one part?
Hint: That part will get flatter.
C) In order to cause a certain part of the cell sheet to bulge, what are three ways to accomplish this?
Hint: Either weaken the tension in that part of the cell sheet, or strengthen the pressure difference there (Or contract more in the concave side of the sheet.
D) In the wall of a cylindrical rubber pipe or balloon, the tension in the circumferential direction is exactly twice as strong in the circumferential direction as in the longitudinal direction, therefore does that mean that cylindrical blood vessels and ducts must contract with twice the force in the circumferential direction as in the longitudinal direction?
Hint: I think so, yes.
E) If you started with a flat sheet of cells, what shape change would be produced if you caused part of it to contract with half the force in one direction as in the direction perpendicular direction?
F) When an epithelial sheet of cells changes from being flat to being a long thin cylinder, what changes in directionality of tension needs to occur in order to produce this shape change? (in a duct or a capillary)
G) If some arbitrary, external force remolds part of a sheet of cells in some way that forces the sheet to become a hollow cylinder, then will it remain cylindrical unless the ratio of tension in perpendicular directions is two to one?
H) Based on looking at an early embryonic brain, how could you determine the relative amounts of tension at different locations and in different directions?
I) What are the curvatures in the computer-generated sheets drawn below?
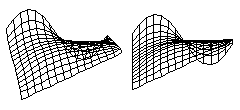
J) Suppose that someone wrote a computer program that simulates shapes produced because of any chosen strengths of tension at every location and direction, could you use this computer program to find out the reasons for the shape of a developing brain, a dividing cell, or a growing cartilage?
K) How could you use such a computer program to test your beliefs about amounts of tension in the brain, etc.
Hint: Does it correctly predict what shape changes are produced by putting an inhibitor (or stimulator) of acto-myosin contractility on different parts of the brain surface.
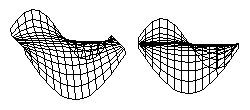
L) Can the flat shape of an ear cartilage be caused by concentrating synthesis of cartilage in certain directions?
Hint: No, because osmotic pressure is a scalar, its strength can't vary with direction; But directional differences in tension can occur.
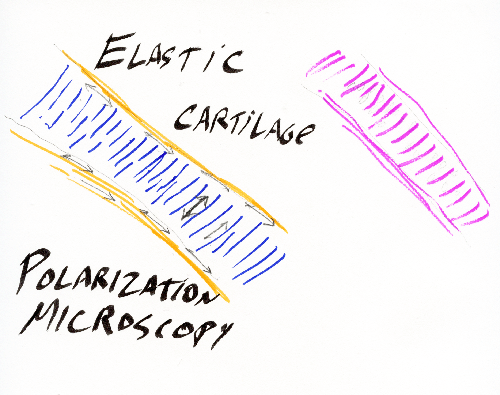
Because electro-osmotic pressure of cartilage is a scalar, it cannot possibly vary with direction. Pressure can vary from one location to another; and that can contribute to shape; but directional expansion has to be mostly caused by weakening of tension in one axis relative to tensions in the perpendicular axes.




7777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777
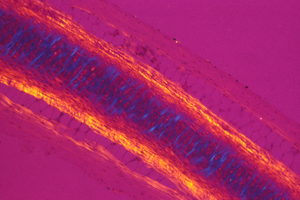
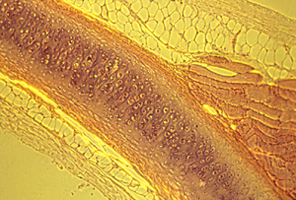
Reducing tensions inside embryos causes spatial irregularities and major birth defects, as extreme as doubling of organs.
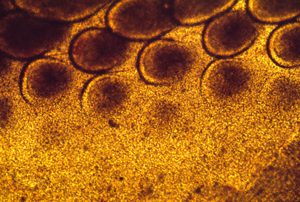
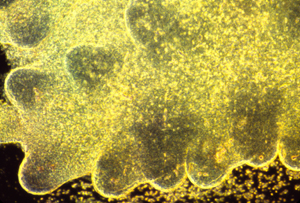
These photographs show the development of the embryonic rudiments of feathers in pieces of bird skin. When the skin develops normally, on the embryo's surface (or if it is kept under mechanical tension) then the feather rudiments form with highly-regular spatial periodicity. But when skin is cultured without the normal amount of mechanical tension, then the feather rudiments form at irregular positions.
Polarized light is one of the only methods by which one can "see" the complicated geometric patterns of mechanical stresses inside developing embryos.

888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888
Although the following is beyond the scope of this course, you may be interested in knowing that one of the advantages of using mechanical forces for the direct control of anatomical patterns is that such mechanisms can directly optimize the geometrical arrangements of organs, for example in the branching patterns of blood vessels.

The links to D'Arcy Thompson's book:
Complete copy of D'Arcy Thompson's book, On Growth and Form
The same book as a text file (no illustrations)
Quote from Adam Wilkins regarding D'Arcy Thompson:
"Any biologist with even a glimmer of genetic knowledge will reject the key idea, the primacy of physical forces in controlling the growth and form of living things.
What this view so conspicuously lacks is a coherent explanation of the differences between like, but non-identical, species and the wealth of data showing the profound effects of different gene mutations on development in a host of organisms."
"At a certain level, we recognize that there is an important element of truth in Thompson's view."
"To ignore the inherent and generic properties of developing organisms is to lose sight of a key element in the dynamics that create recurring shapes and forms in particular fashions."
Pages 396-7 in "The Evolution of Developmental Pathways" Sinauer 2002
What is Wilkins' reasoning?
He assumes forces can't be controlled by genes...
and therefore believes that causation of biological shapes by physical forces would leave genes with no effect on shapes.
Wilkins doesn't realize that genes can change the rules (including equations) that are obeyed by forces of contraction, tension, osmotic pressure, elasticity and many others.
D'Arcy Thompson made a similar mistake.
He doubted that evolution produced anatomical shapes,
and that the real causes were equations like the Young-Pascal "law".
Thompson didn't realize that such equations are over-simplifications, whose details can be changed by natural selection's effects on genes.
101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010
Any point on the surface of a sphere has the same amount of curvature in every direction. We could diagram this situation with circles.
Any point on the surface of a cylinder has zero curvature in two opposite directions, and a constant, non-zero curvature in the two perpendicular directions. This could be diagrammed with a figure 8.
On the surface of a saddle, directional amounts of curvature could be diagrammed as a clover leaf (somewhat like the symbol on the command key of Apples).
The following diagrams illustrate directional variations of second order curvatures.




Thought Question: Consider the shape of what Americans call a football. Could you diagram the directional variations of curvatures on the surface of a football? (Drawing circles and figure-8s of various sizes and orientations.)
What about the surface of a pear? Could you sketch circles, figure-8s and clover-leafs on a pear's surface, so as to represent the directionality and amounts of curvature all over a pear's surface?
What about the surface of a lemon?
What about a conical surface?
Could you do the reverse, and figure out the three-dimensional shape of a solid object, based on diagrams of the amounts of curvature at many different locations.
What about the curvatures of an apple's surface? How are its curvatures changed if someone takes a bite out of it?
Visualize a very small circle in the middle of an area, surrounded by progressively larger circles in the surrounding areas:
Try to sketch a solid 3-dimensional shape whose surface curvatures
correspond to that variation of curvatures.
If the pattern of distribution of little circles indicating curvature has two planes of reflection symmetry, then what symmetry does the physical object have? And the forces would need to have what symmetry in order to create this shape and these curvatures? Please explain how to represent tensions in a sheet of cells stretched between two fixed points, using circles, ellipses, figure-8s.
Finally, please make the same kind of diagram for variations of tensions in a sheet of cells stretched between three points.
And how would this diagram change if the directional force exerted by one of the points were to be changed?
If you like, please invent a puzzle of this kind for me to try to solve. (akh)