Embryology Biology 441 Spring 2011 Albert Harris
Review material for second embryology exam:
Study the following diagrams. Do you understand what they mean?
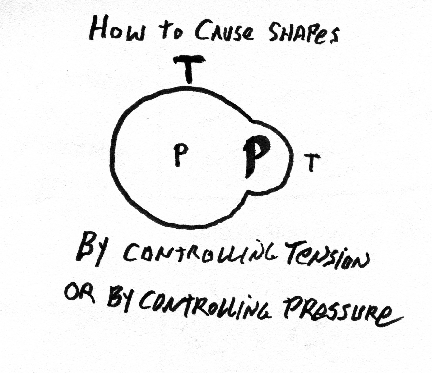
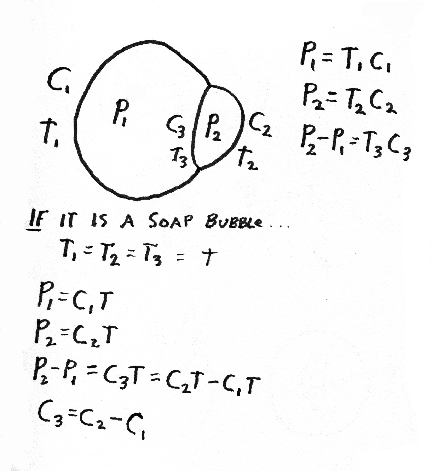
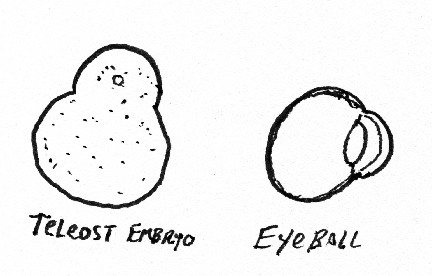
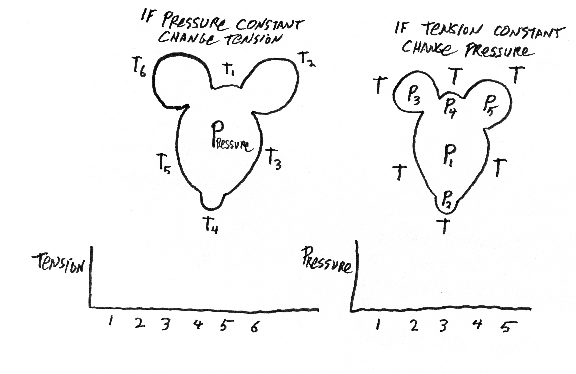
First group of review questions
* indicates more difficult questions.What combination of properties would two diffusible chemicals, A and B, need to have in order to generate regular spatial patterns of lines and dots. Hint, B needs to diffuse faster than A, and the wave-length of the patterns becomes shorter when the ratio of the diffusion rates becomes larger. Are these the only combination of reaction rules and diffusion rates that will generate spatial patterns, starting from homogeneous mixtures of chemicals (no). *Can you figure out any other combinations of effects on each other that could cause chemicals to generate spatial patterns? I will be very impressed if you can; but give this question a few minutes of thought; it's not quite as difficult as it seems.
Such reaction-diffusion systems are methods for "breaking" displacement symmetry; please explain what that means. Alan Turing invented such systems, and also invented the word "morphogen" to refer to the hypothetical chemicals "A" and "B", although he called them X and Y, and hypothesized a more complicated set of effects on each other. Is it true that reaction diffusion systems only magnify random variations in chemical concentrations? (no) [Do many excellent embryologists believe this? Yes]
Please compare what Lewis Wolpert means by "morphogen", in contrast to what Turing originally meant by this word. This difference parallels the distinction between "Positional Information" (in Wolpert's sense) in contrast to what is meant by pre-patterns. What major phenomenon was discovered by Hans Driesch? Imagine that Driesch had instead discovered a mixture of chemicals that were obeying one of the sets of rules that produces reaction-diffusion patterns: then why would/might Driesch have concluded that there was an entelechy in the chemicals?
If some particular kind of embryo normally developed 10 regularly-spaced segments, and when early embryos were cut in two then each half develops 5 segments, instead, is this "regulation" or a failure of regulation? *What if a reaction-diffusion system in a container one inch long produced 10 waves of higher concentration, but in a container one half inch long also produced 10 waves: would that deserve to be called "regulation"? What if the B morphogen usually diffused ten times as fast as the A morphogen (i.e. when the chemicals were in a container one inch long), but if B diffused 20 times faster than A when the chemicals were in a container one-half inch long? The point is that the larger ratio of diffusion constants would cause the wave-length to be half the distance, so the chemicals would produce 10 waves in a half-inch. How would the diffusion rates need to change as a function of container size in order to produce the equivalent of embryonic regulation? *Imagine if a reaction diffusion system somehow produced wave-lengths in the anterior-posterior direction that were linearly proportional to the width of the container (in the dorso-ventral direction). Explain why (or why not) the result would behave like embryonic regulation (as discovered by Driesch).
Please name, and/or draw some objects that have each of the following combinations of symmetry:
- Two planes of reflection symmetry. Four planes of reflection symmetry.
Two-fold rotational symmetry, combined with one plane of reflection symmetry.
Two-fold rotational symmetry, without any planes of reflection symmetry.
Displacement symmetry along one axis. (hint: somites, stripes around a snake, vertebrae.)
A snail shell combines rotational and dilation symmetry: please explain this in terms of Weyl's definition of symmetry.
Continuing this fantasy of being an entelechy, if embryos control organ location by "positional information" (in Wolpert's sense), then how would you need to change the gradients of morphogens in separated embryo halves, or quarters?
The point of these previous two questions is to give you a way to prove that you understand what is meant by regulation, in Driesch's sense, and also understand how Turing's reaction-diffusion theory proposes how periodic patterns or structures are formed, as contrasted with Wolpert's theory of "positional information" as a category of mechanism for controlling the formation of anatomical patterns, and also for explaining the "regulation" of anatomical patterns in embryos that have been separated into halves, etc.
If the bicoid protein is really a morphogen in Wolpert's sense, then what ought to happen if you cut a Drosophila embryo in two, cutting perpendicular to the anterior-posterior axis?
If the concentration gradient of a morphogen formed because messenger RNA for the morphogen was concentrated at one end of the embryo, then how could cutting the embryo into two result in formation of two concentration gradients, each twice as steep as normal? Or can it?
Remembering how the mammal body develops from the primitive streak in the inner cell mass, would you expect a morphogen gradient to have its maximum where the primitive node forms? Or would its minimum form there? Hint: in principle, it could work either way.
Armadillo embryos develop as identical quadruplets, by formation of four primitive streaks in the middle of an inner cell mass, with the heads of the four embryos pointing toward the center, and the tails pointing outward in four perpendicular directions. Suggest how this pattern could be produced by chemical diffusion gradients or Wolpert's positional information.
What is the symmetry of an early armadillo embryo, before each of the quadruplets develops its right-left asymmetry? This symmetry is then changed in what way when all four quadruplets develop their right left asymmetry? In other words, tell what symmetry is possessed by the whole set of quadruplets.
True or false: and explain your reasoning: Reaction-diffusion systems (such as were invented by Turing) are a hypothetical method for reducing ("breaking") the displacement symmetry of developing tissues, in the sense that tissues that previously had infinite displacement symmetry (for displacement by any distance) then have displacement symmetry for certain distances. Hint: true; but you should be able to explain.
Remember the "clock and wave-front" theory of somite formation? What symmetry does it break? Is it fundamentally different than Turing's reaction diffusion system? (hint: I would tend to think yes, it is fundamentally different; but am open to contrary reasoning).
Suppose that you had a strip of tissue that contained two morphogen chemicals, A and B, with A causing increases in both A and B, with B causing decreasing of both A and B, and B diffusing faster than A. You remember what will happen! But next imagine that you start out with a situation in which both A and B are inactive, or don't diffuse, or maybe diffuse at the same rate (so no pattern forms!) but suppose that one end of a strip of tissue acquires these properties first, and then the properties develop progressively, from one end of the strip of tissue, down its length, little by little. Here is the question: what would happen; in particular, would the resulting pattern formation seem like it was caused by a clock and wave-front mechanism? In fact, would it actually BE a special case of a clock and wave-front mechanism? (hint: I welcome either yes or no as answers to this one; but grading will depend on your reasoning; and I realize it's a challenge.)
If you could closely watch development of the four quadruplets of an armadillo, and count somites in each of the 4 embryos, carefully noting the times of separation between somites, how could you hope to use this data to prove or disprove whether the clock and wave-front theory/is what controls somite formation? Likewise, what events in such data could confirm or disprove whether Turing's reaction-diffusion type of mechanism is what controls segmentation of somites?
A more practical experiment would be to dissect two early chicken embryos out of their eggs, into tissue culture dishes, and lay one embryo right on top of the other: then make a time-lapse video of somite segmentation in both embryos. You might need to focus up and down frequently, so as to see both the upper and the lower embryo. Alternatively some very long working distance microscopy might be possible - or confocal microsopy? The goal is to find out whether the embryos somehow influence each other's times of somite separation. For example, these times might tend to synchronize! Would you interpret synchronization as evidence supporting the clock and wave-front hypothesis? Or would synchronization be evidence in favor of control by a reaction-diffusion system? Or would synchronization be predicted by both those theories?
Would it matter whether both embryos were lined up, with heads in the same direction? What if you laid them down at right angles, one perpendicular to the other? What if you laid them down in opposite directions, with the head end of one directly above the tail end of the other embryo? What if you laid them down with the head of one over the neck of the other; or with the head over the middle of the other?
In all cases, we will assume that A and B morphogen chemicals can diffuse the short distances between parts of the embryos directly above and below each other, and will also assume that whatever "clocks" and "wave-fronts" exist will also extent their effects from one embryo to the one above or below it. Assuming that these hypothetical signals will exert effects from one embryo to the closest parts of the other embryo, then what do you expect to happen? What evidence would confirm that the signals from each embryo will sometimes change the time and locations of somite segmentation in the embryo? What do the different theories predict about these induced changes? What differences should there be in these effects, if the axes of the embryos are perpendicular? If the axes are pointed in opposite directions? If the axes are at some other angle? If one embryo is slightly older than the other?
What if you had different mutant strains, one of which formed more somites than the other? Or one of which formed somites faster than the other? ...and you plop one isolated embryo directly on top of the other. The goal is to create a situation in which the different alternative theories make sharply different predictions.
Experiments are more persuasive when you can cause something surprising to happen, the unexpectedness of which can be captured in a single photograph - like if a chick embryo could be stimulated to form somites from the posterior toward the anterior.
Or along the right side sooner and faster than along the other side.
Or more somites on the left than on the right.
What symmetries do each of the following have? And for each one, name something else, NOT on the list, that also has that same symmetry or combination of symmetries.
-
A centipede:
A four bladed propeller:
A plaid piece of cloth:
The color pattern of a Copperhead snake:
A snail shell:
A frog egg before it is fertilized:
A human embryo before it has formed its inner cell mass:
A human embryo after it has formed its inner cell mass, but before a primitive streak has developed:
A human embryo that is developing into identical twins (Don't forget that there are three very different ways in which identical human twins develop):
A gastrulating or a neurulating embryo:
Teeth in a mammal's mouth: (difficult, but you can figure it out)
The individual vertebrae of your backbone:
An individual Dictyostelium slug:
An aggregating mass of Dictyostelium amoebae:
A Dictyostelium fruiting body:
Many Dictyostelium fruiting bodies, of different sizes, as compared with each other:
The mechanism that controls the relative dimensions of fruiting divisions.
Mushrooms:
The letter A
The letter N
The letter H
The symbol %
The symbol *
A zig-zag line
A pluteus larva
A starfish:
Volcanos:
Microscope lenses:
(Old fashioned) balances for weighing things:
Wheatstone bridge electrical circuits for measuring small differences in electrical resistances: And why do they have this symmetry (Don't worry if you haven't had physics, or have forgotten about Wheatstone bridges; but it's no accident they are symmetrical, and I hope you will think about it.
Cumulus clouds in the sky:
The graphs of any equation in which x only occurs as x squared, x to the fourth, or x to other even powers?
The graphs of any equation in which x only occurs as x cubed, x to the fifth power, and simply as x?
The graphs of any equation in which both x and y only appear squared, or to the fourth power.
The graph of x times y is equal to a constant?
In general, how are the symmetries of x and y in an equation related to the symmetry of the graph of an equation? Relate this to Weyl's definition of symmetry.
Argue pro or con: Driesch discovered that whatever mechanisms control pluteus formation, these mechanisms have dilation symmetry.
Argue pro or con: Embryonic development depends on many mechanism that reduce/increase symmetry.
Argue pro or con: Any completely deterministic system keeps whatever symmetry it started with. It can only become less symmetrical by means of some external signal, or by becoming sensitive to random fluctuations, like Brownian movement.
True/false: Cilia and flagella have 9 fold rotational symmetry, but do not have any planes of reflection symmetry.
How is their lack of reflection symmetry (in flagella) related to the asymmetry of the heart and stomach?
Almost half of people with Karteganer's Syndrome have a mirror-image reversal of their aorta, heart, stomach etc. that looks perfectly normal when looked at in a mirror.
What are the five major families of genes that control development of fly anatomy?
What are homeotic mutants? What are two specific examples?
What are hox genes?
What kinds of animals have hox genes?
What is colinearity? Spatial colinearity? Temporal colinearity?
Invent a possible theory/mechanism to explain why colinearity evolved, and why it continues to exist in nearly all multi-cellular animals.
Several researchers have reported that when non-cancerous cells are randomly mixed with cancerous cells derived from the same kind of cells as the non-cancerous cells, then the non-cancerous cells will sort out to an internal position, relative to the cancerous cells, which will form the outside of the aggregate.
Can you suggest why this occurs? Or what it tells us about differences between normal and cancerous cells? (There are many possibilities, that you could invent, based on what you learned previously about chemotaxis, haptotaxis etc.)
In particular, how would Malcolm Steinberg's Differential Adhesion Hypothesis explain such sorting out of cancerous cells from their closest equivalent normal cells?
What other theories have been proposed (locally) to explain why some cell types sort out to internal positions relative to other cell types? And if this alternative hypothesis were correct, then what would that mean about differences between cancerous and normal cells?
What did H. V. Wilson discover? How did he interpret his discovery?
Holtfreter discovered that if you dissect out neural tube ectoderm cells from amphibian embryos of one species, and dissect out somatic ectodermal cells from another species of amphibian, then separate both tissues into single cells (at higher pH), then mix both sets of cells together randomly, and give them a day or two to do whatever they want, then they will form approximately spherical masses, within which all the neural tube ectoderm cells are bunched together in the interior of the masses, surrounded by layers of the somatic ectodermal cells. What do you think this means about the normal mechanism of neurulation? Nothing? That the mechanisms are the same?
If mesoderm is dissected out of gastrulas of one species of frog or salamander, and ectoderm is dissected from gastrulas of another (different color) species of frog or salamander, and them both tissues are separated into their individual cells, and mixed together randomly, would you guess that they would sort out by cell type, or sort out by species? If told that the mesoderm cells consistently sort out to an internal position, surrounded by ectodermal cells, which would you conclude is the cause of the phenomenon, and its significance to the normal mechanisms of embryonic development: That mesodermal cells are more adhesive than ectodermal cells? That mesodermal cells are more strongly contractile? That gastrulation is caused by the same mechanism as causes dissociated, randomly-mixed cells to sort out from each other? That mesodermal cells move to an internal position during gastrulation because they become more adhesive to each other than ectodermal cells are to each other? Or more adhesive to each other than they are to ectodermal cells? Or that mesodermal cells develop stronger contractility? Or suggest any other possible explanations that you can think of.
What are some discoveries made by John Phillip Trinkaus? (There are many)
Why did Prof. Trinkaus decide that the ability of differentiated cells to sort out from each other doesn't or can't tell us anything about normal embryonic development?
How did Rachel Fink explain the ingression of primary mesenchyme cells in sea urchin gastrulation?
What did Stopak and Harris propose is the mechanism by which embryos line up collagen fibers and muscle cells to form the biceps, triceps, gastrocnemius, and all other tendons and skeletal muscles? What was their evidence?
What are some other possible mechanisms that can explain formation of tendons and skeletal muscles? For example, maybe chemotactic attractant substances are secreted at the parts of the surfaces of bones where muscles should attach, and muscle cells are attracted toward these locations? Or perhaps special selective adhesion molecules are secreted at the places on the skeleton where tendons and muscles attach.
Invent experiments that could prove or disprove each of these different hypotheses (or as many of them as possible).
What is the Apical Ectodermal Ridge? Is it found in all types of vertebrate embryos? What happens if it is removed early in limb development?
What is the difference between necrosis and apoptosis? Name at least five phenomena or processes that involve apoptosis.
What are bioassays? (Besides methods for measuring amounts of certain chemicals, using living tissues) What are they really used for? How were bioassays used to discover both the existence, and the chemical structures of auxin, serotonin and many other biologically important signaling chemicals, hormones, vitamins, etc.
How is Prozac related to 2,4-D? Keep thinking! This is a good one. How were they invented? Why do they produce strong effects? What is the same about their inventions?
How does auxin cause positive chemotaxis, negative geotaxis, greater elongation in the dark, increased branching after hedge clipping, and root formation at the bottom of plant cuttings?
Name some other plant hormones.
What is a meristem? What are the two main kinds of meristems?
What is a cambium? What are the two main kinds?
In what sense is a cambium a special kind of meristem?
Why can't plant cells crawl (or gastrulate,, etc.)?
Why is a seed more like a neurula than like an egg?
What are some examples of variables that are scalars?
What are some examples of variables that are vectors?
What are some examples of variables that are second order tensors?
What is an example of a variable that is a fourth order tensor?
(Although lots of very good scientists assume it's a scalar, and
are proud of being "quantitative" when they make this gruesome mistake)
Osmotic pressure is a scalar, but is resisted by collagen fibers, the resistance of which is a tensor (of which order?), therefore the directional elongation of cartilages cannot be caused by the direction of secretion of polysaccharides, and must be caused by directional differences in the strengths of collagen fibers. Please explain and/or argue pro or con.
A good, simple, one-step way to create the shape of the eye and cornea is to exert internal pressure with a gel or liquid, and to have tension be equal everywhere, and in every direction, in the surface layers, except to have tension be weaker in the cornea? Please explain?
Astigmatism of a person's cornea could result from what abnormality of mechanical properties of the embryonic cornea?
If you had a topical drug (colchicine?) that would stimulate increased traction by cornea cells, then how could you use this to replace "lasik surgery"?
Be prepared to draw the following items and mark the principal differences in directional curvature on the surface: light bulb, doughnut, pear, football, coffee mug, wine glass, femur, half-deflated soccer ball, gastrulating sea urchin, embryonic brain, Mickey Mouse balloon, eyeball with cornea
What is meant by the term "model organism"? Why is Drosophila a good one?
What is a genetic screen? What are the main ways in which insect development differs from that of vertebrates?
Professor Harris will not be at UNC Friday afternoon or through the weekend, and will not be checking his e-mail. However, his wife will pass questions on to him. Her address is chlamy@duke.edu